Онлайн расчет объема конуса: Калькулятор для расчета объема конуса

Конус — геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.

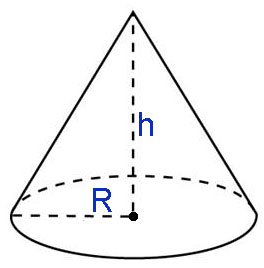
Формула объема конуса через радиус основания и высоту:

• R — радиус оснований конуса.
• h — высота конуса.

 
 
 
 
 
 
 
 
Онлайн калькулятор точного расчета объема конуса:

Инфо урок для 11 класса.

Оцени статью

Оценить

Средняя оценка / 5. Количество голосов:

Спасибо, помогите другим — напишите комментарий, добавьте информации к статье.

Или поделись статьей

Видим, что вы не нашли ответ на свой вопрос.

Помогите улучшить статью.

Напишите комментарий, что можно добавить к статье, какой информации не хватает.

Отправить

Спасибо за ваши отзыв!

Онлайн калькулятор: Объем геометрических фигур

Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.

Объем куба

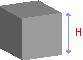Размеры куба

Формула:

Объем куба

Длина ребра куба (H)

Точность вычисления

Знаков после запятой: 5

save Сохранить extension Виджет

Объем прямоугольной призмы

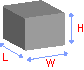Размеры прямоугольной призмы

Формула:

Объем прямоугольной призмы

Точность вычисления

Знаков после запятой: 5

save Сохранить extension Виджет

Объем пирамиды

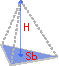Размеры пирамиды

Формула:

Объем пирамиды

Площадь основания

Точность вычисления

Знаков после запятой: 5

save Сохранить extension Виджет

Объем усеченной пирамиды

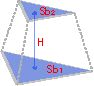Размеры усеченной пирамиды

Формула:

Объем усеченной пирамиды

Точность вычисления

Знаков после запятой: 5

Калькулятор объема

Ниже приведен список калькуляторов объема для нескольких распространенных фигур. Пожалуйста, заполните соответствующие поля и нажмите кнопку «Рассчитать».

Калькулятор объема сферы

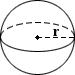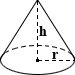
Калькулятор объема конуса

Cube Volume Calculator

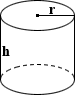
Калькулятор объема цилиндра

Прямоугольный калькулятор объема бака

Калькулятор объема капсулы

Калькулятор объема сферической крышки

Пожалуйста, укажите любые два значения ниже для расчета.

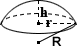Конус Frustum Объем Калькулятор

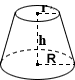Ellipsoid Volume Calculator

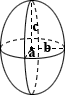Калькулятор объема квадратной пирамиды

Tube Volume Calculator

Калькулятор площади поверхности | Калькулятор площади

Объем — это количественное определение трехмерного пространства, которое занимает вещество.Единицей СИ для объема является кубический метр или м ³ . По общему правилу объем контейнера, как правило, зависит от его вместимости и количества жидкости, которое он способен удерживать, а не от объема пространства, которое вытесняет реальный контейнер. Объемы многих форм могут быть рассчитаны с помощью четко определенных формул. В некоторых случаях более сложные формы могут быть разбиты на их более простые совокупные формы, а сумма их объемов используется для определения общего объема. Объемы других, даже более сложных форм, можно рассчитать с помощью интегрального исчисления, если для границы формы существует формула.Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и является однородной, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых наиболее распространенных простых форм.

Сфера

Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, которые равноудалены от данной точки в ее центре, где расстояние между центром и любой точкой на сфере равно радиусу r .Скорее всего, наиболее известным сферическим объектом является идеально круглый шар. В математике существует различие между шаром и сферой, где шар состоит из пространства, ограниченного сферой. Независимо от этого различия шар и сфера имеют одинаковый радиус, центр и диаметр, и их объемы одинаковы. Как и в случае с кругом, самый длинный отрезок линии, соединяющий две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема сферы приведено ниже:

EX: Клэр хочет заполнить идеально сферический водяной шар радиусом 0.15 футов с уксусом, чтобы использовать его в борьбе с ее заклятым врагом Хильдой в эти выходные. Необходимый объем уксуса может быть рассчитан с использованием приведенного ниже уравнения:

объем = 4/3 × π × 0,15 ³ = 0,141 фут ³

Конус

Конус — это трехмерная форма, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус формируется аналогично кругу с помощью набора отрезков, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, которая содержит окружность (или какую-либо другую базу).На этой странице рассматривается только случай конечного правого кругового конуса. Конусы, состоящие из полулиний, некруглых оснований и т. Д., Которые простираются бесконечно, не будут рассматриваться. Уравнение для расчета объема конуса выглядит следующим образом:

, где r — радиус, а h — высота конуса

EX: Беа намерена выйти из магазина мороженого, с трудом заработав 5 долларов. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, несомненно, больше.Она определяет, что она предпочитает обычные сахарные шишки на 15% больше, чем вафельные, и должна определить, является ли потенциальный объем вафельного рожка на ≥ 15% больше, чем у сахарного рожка. Объем вафельного рожка с круглым основанием с радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать по приведенному ниже уравнению:

объем = 1/3 × π × 1,5 ² × 5 = 11,781 в ³

Bea также вычисляет объем сахарного рожка и находит, что разница составляет <15%, и решает приобрести сахарный рожок.Теперь все, что ей нужно сделать, это использовать свое ангельское, детское обращение, чтобы манипулировать посохом, чтобы опустошать контейнеры с мороженым в ее конус.

куб

Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых встречаются в каждой из его вершин, и все они перпендикулярны своим соответствующим смежным граням. Куб является частным случаем многих классификаций форм в геометрии, включая квадратный параллелепипед, равносторонний кубоид и правый ромбоэдр.Ниже приведено уравнение для расчета объема куба:

Объем

= ³
где a — длина ребра куба

EX: Боб, который родился в штате Вайоминг (и никогда не покидал штат), недавно посетил свою исконную родину в штате Небраска. Боб, пораженный великолепием штата Небраска и окружающей средой, непохожий на то, что он испытывал ранее, знал, что ему нужно взять с собой часть Небраски. У Боба кубический чемодан с длиной ребра 2 фута, и он рассчитывает объем почвы, который он может взять с собой домой, следующим образом:

объем = 2 ³ = 8 футов ³

Цилиндр

Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от заданной оси прямой линии.Однако в общем использовании «цилиндр» относится к правому круглому цилиндру, где основания цилиндра представляют собой окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой h и радиусом r . Уравнение для расчета объема цилиндра приведено ниже:

объем = πr ² ч
где r — радиус, а h — высота резервуара

EX: Келум хочет построить замок из песка в гостиной своего дома.Поскольку он является твердым сторонником переработки отходов, он извлек три цилиндрических бочки с места незаконного сброса и очистил химические отходы от бочек, используя моющее средство для мытья посуды и воду. Каждый из бочек имеет радиус 3 фута и высоту 4 фута, и Caelum определяет объем песка, который может вместить каждый, используя уравнение ниже:

объем = π × 3 ² × 4 = 113,097 футов ³

Он успешно строит замок из песка в своем доме, и в качестве дополнительного бонуса ему удается экономить электроэнергию при ночном освещении, так как его замок из песка светится ярко-зеленым в темноте.

Прямоугольный резервуар

Прямоугольный резервуар представляет собой обобщенную форму куба, где стороны могут иметь различную длину. Он ограничен шестью гранями, три из которых встречаются в его вершинах, и все они перпендикулярны их соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:

объем = длина × ширина × высота

EX: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к пирогу.Она планирует отправиться в поход по тропе Калалау в Кауаи, и, хотя она очень подходит, Дарби беспокоится о своей способности завершить тропу из-за отсутствия пирога. Она решает упаковать только самое необходимое и хочет наполнить свою идеально прямоугольную пачку длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно, тортиком. Точный объем торта, который она может поместить в свою пачку, рассчитывается ниже:

объем = 2 × 3 × 4 = 24 фута ³

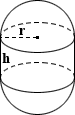
Капсула

Капсула представляет собой трехмерную геометрическую форму, состоящую из цилиндра и двух полусферических концов, где полусфера представляет собой половину сферы.Отсюда следует, что объем капсулы можно рассчитать путем объединения уравнений объема для сферы и правого круглого цилиндра:

Объем

= 2 ч +

№ 3 = № 2 (

р + ч)

, где r — радиус, а h — высота цилиндрической части

EX: Учитывая капсулу с радиусом 1,5 фута и высотой 3 фута, определите объем расплавленного молочного шоколада, который Джо может нести в капсуле времени, которую он хочет похоронить для будущих поколений, на своем пути самопознания через Гималаи:

объем = π × 1.5 ² × 3 + 4/3 × π × 1,5 ³ = 35,343 фута ³

Сферическая крышка

Сферическая крышка — это часть сферы, которая отделена от остальной части сферы плоскостью. Если плоскость проходит через центр сферы, сферическая крышка называется полусферой. Существуют и другие различия, в том числе сферический сегмент, где сфера сегментирована с двумя параллельными плоскостями и двумя разными радиусами, где плоскости проходят через сферу. Уравнение для расчета объема сферического колпачка получено из уравнения сферического сегмента, где второй радиус равен 0.По отношению к сферической крышке, показанной в калькуляторе:

Учитывая два значения, калькулятор вычисляет третье значение и объем. Уравнения для преобразования высоты в радиусы приведены ниже:

Дано r и R : h = R ± √R ² — r ²

Дано R и h : r = √2Rh — h ²
где r — радиус основания, R — радиус сферы, а h — высота сферического колпачка

EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы практиковать, решает саботировать мяч для гольфа Джеймса.Он отсекает идеальную сферическую крышку от верхней части мяча для гольфа Джеймса, и ему необходимо рассчитать объем материала, необходимый для замены сферической крышки и исказить вес мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую Джек отрезал, составляет 0,3 дюйма, объем можно рассчитать следующим образом:

объем = 1/3 × π × 0,3 ² (3 × 1,68–0,3) = 0,447 в ³

К сожалению для Джека, Джеймс случайно получил новую партию шаров за день до их игры, и все усилия Джека были напрасны.

Конический усеченный

Коническая усеченная часть — это часть твердого тела, которая остается при разрезании конуса двумя параллельными плоскостями. Этот калькулятор рассчитывает объем для правого круглого конуса специально. Типичные конические усеченные контуры, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы. Объем правого конического усеченного конуса рассчитывается по следующему уравнению:

объем =

πh (r 2 + rR + R 2 )

, где r и R — радиусы оснований, h — высота усеченного конуса

EX: Bea успешно приобрела немного мороженого в сахарном конусе и только что съела его таким образом, чтобы мороженое было упаковано внутри конуса, а уровень поверхности мороженого был параллелен плоскости отверстия конуса.Она собирается съесть свой конус и оставшееся мороженое, когда ее брат схватил ее конус и откусил часть нижней части конуса, которая идеально параллельна ранее единственному отверстию. Теперь у Bea осталось мороженое с утечкой в ​​правом конусе, и она должна рассчитать объем мороженого, которое она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма, с радиусами 1,5 дюйма и 0,2 дюйма:

объем = 1/3 × π × 4 (0,2 ² + 0,2 × 1,5 + 1,5 ² ) = 10.849 в ³

Эллипсоид

Эллипсоид является трехмерным аналогом эллипса и является поверхностью, которая может быть описана как деформация сферы посредством масштабирования направленных элементов. Центр эллипсоида — это точка, в которой пересекаются три попарно перпендикулярных оси симметрии, а отрезки, ограничивающие эти оси симметрии, называются основными осями. Если все три имеют различную длину, эллипсоид обычно описывается как трехосный.Уравнение для расчета объема эллипсоида выглядит следующим образом:

, где a , b и c являются длинами осей

EX: Хабат любит есть только мясо, но его мать настаивает на том, что он потребляет слишком много, и позволяет ему есть столько мяса, сколько он может вместить в булочку эллипсоидной формы. Таким образом, Xabat выдавливает булочку, чтобы максимизировать объем мяса, которое он может поместить в свой бутерброд. Учитывая, что его булочка имеет длину оси 1.5 дюймов, 2 дюйма и 5 дюймов, Xabat рассчитывает объем мяса, которое он может поместить в каждую выдолбленную булочку, следующим образом:

объем = 4/3 × π × 1,5 × 2 × 5 = 62,832 в ³

Квадратная пирамида

Геометрическая пирамида — это трехмерное тело, образованное путем соединения полигонального основания с точкой, называемой его вершиной, где многоугольник — это форма в плоскости, ограниченной конечным числом отрезков прямых линий. Существует много возможных многоугольных оснований для пирамиды, но квадратная пирамида — это пирамида, в которой основание — это квадрат.Другое различие, связанное с пирамидами, касается расположения вершины. Правая пирамида имеет вершину, которая находится прямо над центром тяжести своего основания. Независимо от того, где находится вершина пирамиды, пока ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды можно записать как:

Обобщенный объем пирамиды:

Калькулятор конуса

Форма конуса

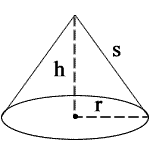
r = радиус
h = высота
с = наклонная высота
V = объем
L = площадь боковой поверхности
B = площадь поверхности основания
A = общая площадь поверхности
π = pi = 3.1415926535898
√ = квадратный корень

Калькулятор

Использование

Этот онлайн-калькулятор рассчитает различные свойства правильного круглого конуса с учетом любых 2 известных переменных. Термин «круговой» поясняет эту форму в виде пирамиды с круглым поперечным сечением. Термин «право» означает, что вершина конуса центрирована над основанием. Использование термина «конус» само по себе часто означает правильный круглый конус.

Единицы: Обратите внимание, что единицы показаны для удобства, но не влияют на расчеты. Единицы измерения установлены для указания порядка результатов, таких как футы, футы ² или футы ³ . Например, если вы начинаете с мм и знаете r и h в мм, ваши вычисления приведут к s в мм, V в мм ³ , L в мм ² , B в мм ² и A в мм ² .

Ниже приведены стандартные формулы для конуса.Расчеты основаны на алгебраических манипуляциях с этими стандартными формулами.

Формулы круглого конуса в терминах радиуса r и высоты h:

• Объем конуса:
• Скошенная высота конуса:
• Площадь боковой поверхности конуса:
  • L = πrs = πr√ (r ² + h ² )
• Площадь базовой поверхности конуса (круг):
• Общая площадь поверхности конуса:
  • A = L + B = πrs + πr ² = πr (s + r) = πr (r + √ (r ² + h ² ))

Расчет круглого конуса:

Используйте следующие дополнительные формулы вместе с формулами выше.

• По заданному радиусу и высоте рассчитайте наклонную высоту, объем, площадь боковой поверхности и общую площадь поверхности.
  Дано r, h найти s, V, L, A
• По заданному радиусу и высоте наклона рассчитайте высоту, объем, площадь боковой поверхности и общую площадь поверхности.
  Даны r, s найти h, V, L, A
• По заданному радиусу и объему рассчитайте высоту, высоту уклона, площадь боковой поверхности и общую площадь поверхности.
  По заданному r, V найти h, s, L, A
• По заданному радиусу и площади боковой поверхности рассчитайте высоту, высоту наклона, объем и общую площадь поверхности.
  Дано г, L найти ч, с, V, A
  • с = L / (πr)
  • h = √ (с ² — r ² )
• По заданному радиусу и общей площади поверхности рассчитывают высоту, высоту уклона, объем и площадь боковой поверхности.
  Учитывая г, А найти ч, с, V, L
  • с = [A — (πr ² )] / (πr)
  • h = √ (с ² — r ² )
• По заданной высоте и наклонной высоте рассчитайте радиус, объем, площадь боковой поверхности и общую площадь поверхности.
  Дано h, s найти r, V, L, A
• По заданной высоте и объему рассчитайте радиус, наклонную высоту, площадь боковой поверхности и общую площадь поверхности.
  Дано h, V найти r, s, L, A
  • r = √ [(3 * v) / (π * h)]
• По заданной высоте наклона и площади боковой поверхности рассчитайте радиус, высоту, объем и общую площадь поверхности.
  Дано s, L найти r, h, V, A
  • r = L / (π * s)
  • h = √ (с ² — r ² )

Отзывы

Вайштайн, Эрик У.«Конус». От MathWorld — веб-ресурс Wolfram.
http://mathworld.wolfram.com/Cone.html

,

Объем конусного калькулятора

Объем конуса формула

Формула для объема конуса равна (высота x π x (диаметр / 2) ² ) / 3 , где (диаметр / 2) — радиус основания (d = 2 xr), поэтому другое способ записи это (высота х π х радиус ² ) / 3 , как видно на рисунке ниже:

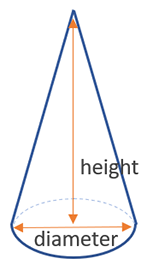
Несмотря на относительную сложность тела, вам нужно только два измерения для расчета объема конуса: его высота и диаметр его основания или, что эквивалентно, — его радиус.π — математическая постоянная без единиц, равная ~ 3.149159.

Как рассчитать объем конуса?

Сначала выполните измерение диаметра (самое широкое измерение основания), затем измерьте или оцените высоту. Если у вас уже есть планы или схемы, просто получите длины оттуда. Преобразовать единицы длины в одну и ту же базу, например дюймов или сантиметров, затем следуйте приведенной выше формуле или воспользуйтесь нашим онлайн-калькулятором конусов. Вывод всегда в кубических единицах, т.е.грамм. кубических дюймов, кубических футов, кубических ярдов, кубических мм, кубических сантиметров, кубических метров и так далее.

Пример: найти объем конуса

Применение уравнений объема конуса является простым, при условии, что высота конуса известна, и также дается одно из следующего: радиус, диаметр или площадь его основания. Например, если высота и площадь задаются равными 2 футам и 15 квадратным футам, то объем конуса будет просто результатом умножения двух и деления на три: 2 x 15/3 = 30/3 = 10 кубических футов.

Использование второго уравнения целесообразно, если область неизвестна, но радиус может быть измерен или задан. Расчет объема требует только одного дополнительного шага. Например, если высота равна 20 дюймам, а радиус равен 4 дюймам, площадь можно рассчитать как 3,14159 x 4 ² = 3,14159 x 16 = 50,265. Тогда объем составляет 20 х 50,26544 / 3 = 1005,31 / 3 = 335,1 куб. Дюйма. Более высокий уровень точности для π приведет к более точным результатам, поэтому использование калькулятора объема конуса является предпочтительным.

Практические применения

Конус не так популярен, как некоторые другие органы в строительстве и машиностроении, но он имеет свои применения. Одним из первых примеров, которые вы можете вспомнить, являются дорожные конусы, которые могут быть заполнены водой или другим материалом, чтобы держать их на месте, особенно в ветреных местах.

,

Площадь, объем и наклонная высота конусного калькулятора

Решенный пример

Решенная ниже примерная задача может быть полезна для понимания того, как значения используются в математических формулах для определения площади, объема и наклонной высоты правого круглого конуса.

Пример задачи:
Найти площадь, объем и наклонную высоту правого круглого конуса с радиусом основания и высотой 15 см и 7 см соответственно?

Решение:
Заданные значения
базовый радиус r = 15 см
высота h = 7 см

Пошаговый расчет
формула для нахождения площади = πr [r + √ (r ² + h ² )]
подставляют значения
= π x 15 x [15 + √ (15 ² + 7 ² )]
= 1487.49 см ²

формула для определения объема = (1/3) πr ² ч
подставим значения
= (1/3) x π x 15 ² x 7
= 1650 см ³

Возможно, потребуется рассчитать площадь, объем и наклонную высоту конуса в СИ или в метрических или обычных единичных системах США, поэтому этот конусный калькулятор оснащен функцией преобразования основных единиц измерения для нахождения выходных значений в различных обычных единицы измерения, такие как дюймы (дюймы), футы (футы), метры (м), сантиметры (см) и миллиметры (мм), с помощью приведенной ниже таблицы пересчета.

10 мм = 1 см 100 мм = 3,93 в 1000 мм = 3,28 фута 1000 мм = 1 м

1 см = 10 мм 10 см = 3,93 в 100 см = 3,28 фута 100 см = 1 м

1 фут = 3048 мм 1 фут = 304,8 см 1 фут = 12 в 10 фут = 3,048 м

1 дюйм = 25,4 мм 1 дюйм = 2,54 см 100 дюймов = 8,33 фута 100 дюймов = 2,54 м

В области геометрических расчетов , определение площади, объема и наклонной высоты конуса очень важно для понимания части базовой математики.Приведенные выше формулы, пошаговые вычисления и решенный пример могут помочь пользователям понять, как вручную рассчитать площадь, объем и наклонную высоту конуса, однако, когда дело доходит до оперативного выполнения быстрых вычислений, этот калькулятор конусов может быть полезен чтобы найти результаты. ,