Как найти Объем Параллелепипеда?
Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.
Два свойства объёма
|
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Объем прямоугольного параллелепипеда
Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.
Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.
Формула объема прямоугольного параллелепипеда Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты: V = a × b × h |
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.
a | длина параллелепипеда |
b | ширина параллелепипеда |
h | высота параллелепипеда |
P (осн) | периметр основания |
S (осн) | площадь основания |
S (бок) | площадь боковой поверхности |
S (п. | площадь полной поверхности |
V | объем |
Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.
a = 9 см
b = 6 см
h = 3 см
V = a × b × h
V = 9 × 6 × 3 = 162 см3.
Ответ: объем прямоугольного параллелепипеда равен 162 см
Следствие Объем параллелепипеда равен произведению площади основания на высоту. V = Sосн × h |
Из этого следствия выведем формулу нахождения площади основания параллелепипеда.
Sосн = V : h
Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 96 см3, а высота 8 см.
V = 96 см3
h = 8 см
V = Sосн × h
Sосн = V : h
Sосн = 82 см3 : 8 см = 12 см2.
Ответ: площадь основания параллелепипеда равна 12 см2.
Обучение на курсах по математике в онлайн-школе Skysmart поможет быстрее разобраться в теме и правильно решать задачки!
Вычисление площади
Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.
Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.
Так как противолежащие грани прямоугольного параллелепипеда одинаковые, то получим формулу:
Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания. Так как площади оснований у прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sп. п. = 2 (ab + ac + bc)
Пример 3. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (6 × 4 + 6 × 3 + 4 × 3) = 2 × (24 + 18 + 12) = 2 × 54 = 108 см2.
Ответ: площадь поверхности параллелепипеда — 108 см
Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно.
Задачи на самопроверку
Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.
Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.
Как решаем:
a = 18 см
b = 10 см
h = 7 см
Формула нахождения объема параллелепипеда:
V = a × b × h
Подставляем наши числа:
V = 18 × 10 × 7 = 1260 см3.
Ответ: объём параллелепипеда равен 1260 см
Задачка 2. Найдите площадь основания параллелепипеда, если его объём равен 120 см3, а высота — 15 см.
Как решаем:
V = 120 см
h = 15 см
V = Sосн × h
Sосн = V : h
Sосн = 120 см3: 15 см = 8 см2.
Ответ: площадь основания параллелепипеда равна 8 см2.
Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания равна 30 сантиметров, ширина равна 12 см, а высота равна 5 см.
Как решаем:
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см2.
Ответ: площадь полной поверхности параллелепипеда равна 1140 см2.
Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.
V параллелепипеда | V = a × b × h |
| V = Sосн × h |
S боковой поверхности | Sб. |
S полной поверхности | Sп. п. = 2 (ab + ac + bc) |
Объем, Площадь поверхности, формулы объема
Стандартное обозначение объема есть V.
Этим мы измеряем количество (наример, воды), которая может заполнить фигуру.
Только пространственные фигуры имеют объем. Например, треугольники, квадраты не имеют объема, но шар имеет объем (потому что он может быть заполнен чем-то, например водой).
Прямоугольный параллелепипед
Прямоугольный параллелепипед это фигура, все стороны которой — прямоугольники.
тогда формула объема есть:
$V = a \cdot b \cdot c$
Площадь поверхности:S = $2(a \cdot b + a \cdot c + b \cdot c)$
Куб
Куб есть параллелепипедом, все ребра (стороны) которого равны.
Если длина стороны куба равна a, тогда формула объема:
$V = a. 2 \cdot h$
2 \cdot h$
$S = 2\cdot\pi\cdot r \cdot h$
Площадь полной поверхности:$S = 2\cdot\pi\cdot r(h + r)$
Тест: объём и площадь поверхности
Формулы объема и программы для расчета объема
Содержание:
Формула объема куба
1) Объем куба равен кубу его ребра.
V — объем куба
H — высота ребра куба
См. также: Программа для расчета объема куба.
Формула объема пирамиды
1) Объем пирамиды равен одной трети произведения площади основания S (ABCD) на высоту h (OS).
V — объем пирамиды
S — площадь основания пирамиды
h — высота пирамиды
См. также: Программа для расчета объема пирамиды.
также: Программа для расчета объема пирамиды.
Формулы объема конуса
1) Объем конуса равен одной трети произведения площади основания на высоту.
2) Объем конуса равен одной трети произведения числа пи (3.1415) на квадрат радиуса основания на высоту.
V — объем конуса
S — площадь основания конуса
h — высота конуса
π — число пи (3.1415)
r — радиус конуса
См. также: Программа для расчета объема конуса.
Формулы объема цилиндра
1) Объем цилиндра равен произведению площади основания на высоту.
2) Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
V — объем цилиндра
S — площадь основания цилиндра
h — высота цилиндра
π — число пи (3.1415)
r — радиус цилиндра
См. также: Программа для расчета объема цилиндра.
также: Программа для расчета объема цилиндра.
Формула объема шара
1) Объем шара вычисляется по приведенной ниже формуле.
V — объем шара
π — число пи (3.1415)
R — радиус шара
См. также: Программа для расчета объема шара.
Формула объема тетраэдра
1) Объем тетраэдра равен дроби в числителе которой корень квадратный из двух помноженный на куб длины ребра тетраэдра, а в знаменателе двенадцать.
V — объем тетраэдра
a — длина ребра тетраэдра
См. также: Программа для расчета объема тетраэдра.
Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Рассчитать объем коробки в м3 и литрах онлайн
07.10.2019Сколько будет стоить отправка вашего груза до места назначения? Чтобы ответить на это вопрос, нужно знать его объем в кубических метрах, т. к. транспортные компании чаще всего в прайсе указывают стоимость услуг именно в таких единицах измерения.
к. транспортные компании чаще всего в прайсе указывают стоимость услуг именно в таких единицах измерения.
Картонные коробки — наиболее выгодный и удобный вид упаковки для большинства товаров. Выбирая гофроупаковку для своей продукции, вам нужно, в первую очередь, рассчитать объем коробок и заказать нужное количество коробок, чтобы не перевозить воздух и не переплачивать за транспортные услуги.
Если в результате расчета оказалось, что вам требуется гофротара индивидуальных размеров, наша компания «МС-ПАК» изготовит нужный тираж на заказ. Рассмотрим, как правильно рассчитать объем картонной коробки.
Поэтапный расчет объема картонной коробки
Для расчета нужно:
- Измерить длину а и ширину b, если дно коробки квадратное, то а=b;
- Измерить высоту h как расстояние от нижнего до верхнего клапана коробки.
Сначала нужно рассчитать внутренний объем коробки, необходимый для размещения груза. Габаритные размеры груза должны быть на 5–10 мм меньше, чем внутренние размеры гофроупаковки.
Габаритные размеры груза должны быть на 5–10 мм меньше, чем внутренние размеры гофроупаковки.
V=a*b*h
где a – длина основания (м), b – ширина основания (м),
h – высота коробки (м).
V=S*h
где S — площадь основания коробки, а h — ее высота.
Объем, занимаемый заготовкой (коробкой) (с учетом толщины стенок) рассчитывается для правильного размещения внутри транспортного средства или хранения на складе.
Формула для расчета занимаемого объема:
V=Площадь (S) * толщину листа
*как рассчитать площадь (S) картонной коробки — в этой статье
| Тип: | Профиль: | Толщина (мм): |
| Трехслойный гофрокартон | B | 3 |
| Трехслойный гофрокартон | C | 3,7 |
| Трехслойный гофрокартон | E | 1,6 |
| Пятислойный гофрокартон | BC | 7 |
| Пятислойный гофрокартон | BE | 4 |
Перемножив полученные значения, получим объем коробки в кубических метрах. Чтобы получить результат в литрах необходимо полученное значение в м3 умножить на 1000.
Чтобы получить результат в литрах необходимо полученное значение в м3 умножить на 1000.
Рассчитать объем коробки в м
3 и литрах онлайнДля обычных коробок в форме куба или параллелепипеда (со сторонами в виде квадратов или прямоугольников) на нашем сайте есть онлайн-калькулятор, который ускорит расчет.
Пример расчета
После измерения получены значения: а=600 мм, b=400 мм, h= 400 мм.
Переводим их в метры: а=600/1000=0,6 м, b=400/1000=0,4 м, h=400/1000=0,4 м.
Подставляя полученные результаты в формулу для расчета объема, получим значение: V=a*b*h=0,6*0,4*0,4=0,096 м3.
Если в коробки фасуются сыпучие или жидкие грузы, то для расчета необходимого объема используем соотношение 1 м3 = 1000 л и, умножив полученное значение объема в м3 на 1000, получим объем в литрах.
Для нашего примера объем коробки (внутренний) в литрах равен 0,096*1000=96 литров.
Периметр, площадь и объем
Данный материал содержит геометрические фигуры с измерениями.Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Периметр геометрической фигуры
Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:
P = 9 см + 4 см + 9 см + 4 см = 26 см.
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
P = 5 см × 4 = 20 см
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
Допустим, потребовалось измерить площадь следующей комнаты:
Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:
В данном случае площадь удобно измерить в квадратных метрах:
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:
Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
Теперь измерим ширину. Пусть она составила 3 метра:
Умножим длину (4 м) на ширину (3 м).
4 × 3 = 12
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
S = a2
где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».
Например, вычислим площадь квадрат со стороной 2 см.
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».
Вычислим площадь квадрата со стороной 3 метра
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
S = a × b
Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.
Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см
Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.
Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:
3 а = 100 м2 × 3 = 300 м2
В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:
1 сотка = 100 м2
2 сотки = 200 м2
10 соток = 1000 м2
Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:
20 га = 10 000 м2 × 20 = 200 000 м2
Прямоугольный параллелепипед и куб
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:
На рисунке показан прямоугольный параллелепипед:
Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
V = 12 см3
Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
V = 3 × 3 × 3 = 27 см³
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
V = 33 = 27 см3
Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
Таким образом, объём куба вычисляется по следующему правилу:
V = a3
Где a — длина куба.
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).
Другое название одного кубического дециметра – один литр.
1 дм3 = 1 литр
Перевод единиц измерения объёма
Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.
Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см
Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:
V = 1003 = 1 000 000 см3
Получается, что на один кубический метр приходится один миллион кубических сантиметров:
1 м3 = 1 000 000 см3
Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.
Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.
А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.
Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»
300 000 000 см3 : 1 000 000 см3 = 300 м3
Пример 2. Выразить 3 м3 в кубических сантиметрах.
Умножим 3 м3 на 1 000 000
3 м3 × 1 000 000 = 3 000 000 см3
Пример 3. Выразить 60 000 000 см3 в кубических метрах.
Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3
Для этого разделим 60 000 000 см3 на 1 000 000 см3
60 000 000 см3 : 1 000 000 см3 = 60 м3
Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
1 литр = 1 дм3
Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.
Пример 1. Перевести 5 литров в кубические дециметры.
Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1
5 л × 1 = 5 дм3
Пример 2. Перевести 6000 литров в кубические метры.
Шесть тысяч литров это шесть тысяч кубических дециметров:
6000 л × 1 = 6000 дм3
Теперь переведём эти 6000 дм3 в кубические метры.
Длина, ширина и высота одного кубического метра равны 10 дм
Если вычислить объём этого куба в дециметрах, то получим 1000 дм3
V = 103= 1000 дм3
Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
6 000 дм3 : 1 000 дм3 = 6 м3
Значит, 6000 л = 6 м3.
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.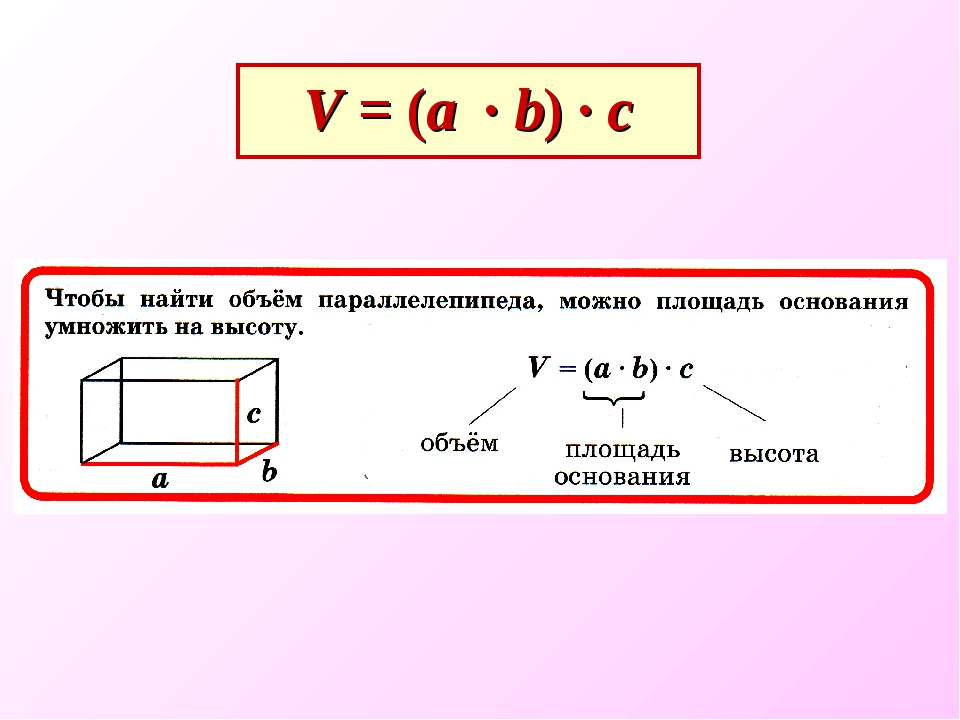
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
242 = 576
Таблица кубов
Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
353 = 42875
Задания для самостоятельного решения
Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.
Решение
P = 2(a + b)
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.
Решение
S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2
Ответ: площадь равна 12 см2.
Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.
Решение
S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2
Ответ: ширина прямоугольника составляет 2 см.
Задача 4. Вычислите площадь квадрата со стороной 8 см
Решение
S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2
Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.
Решение
V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3
Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см
Решение
V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4
Ответ: высота прямоугольного параллелепипеда равна 4 см.
Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
4 × 3 = 12 га
Ответ: пшеницей засеяно 12 га.
Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.Решение
a — длина
b — ширина
c — высота
a = 42 м
b = м
c = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм3
35 525 л = 35 525 дм3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
35 525 дм3 : 1000 дм3 = 35,525 м3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
V = 35,525
a = 5.8
b = 3.5
c = x
35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м
с = 1,75
Ответ: высота (глубина) бассейна составляет 1,75 м.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Как правильно рассчитать объем коробки?
Коробка служит тарой для перевозки многих предметов. В бизнесе при доставке товаров используют коробки разных размеров и форм. Тара помогает сохранить внешний вид продуктов при транспортировке. При заказе средств перевозки должны точно знать объем перевозимых товаров. Если тарой служит коробка, то следует определить ее объем. Как правильно рассчитать объем коробки, чтобы вычислить объем груза, узнаем из нижеприведенной статьи.
Если тарой служит коробка, то следует определить ее объем. Как правильно рассчитать объем коробки, чтобы вычислить объем груза, узнаем из нижеприведенной статьи.
Содержание:
- Формы коробки
- Как измерить коробку для вычисления ее объема
- Какие формулы можно использовать при расчете объема коробки
- Облегченные расчеты объема коробок онлайн
Формы коробки
Легко сосчитать объем кубической коробки, перемножив величину стороны на три. На практике применяются разные формы коробок:
- Прямоугольная;
- Кубическая;
- Цилиндрическая;
- Пирамидальная (в виде усеченной пирамиды).
Как измерить коробку для вычисления ее объема
Для определения объема коробки следует снять замеры размеров сторон. Замеры проводить в одной определенной величине: в миллиметрах, сантиметрах, дециметрах. Конечный итог объема переводим в международный стандарт – кубические метры.
Какие формулы можно использовать при расчете объема коробки
Для каждой формы коробки существует определенная форма расчета объема. Несмотря на то, что на сайтах есть калькуляторы расчета объема, нужно знать, по каким формулам рассчитывают объем каждого вида коробки.
Несмотря на то, что на сайтах есть калькуляторы расчета объема, нужно знать, по каким формулам рассчитывают объем каждого вида коробки.
Объем прямоугольной коробки
Сначала нам нужно измерить длину коробки. Прикладываем сантиметр или линейку к самой длинной стороне. Полученный результат длины – l записываем. Самая короткая сторона – это ширина. Аналогично проводим замер, записываем результат буквой w. Далее определяем высоту – h, которую замеряем от высшей точки коробки до низшей.
Объем вычисляем по известной формуле: v = l х w х h, где v – объем коробки. Наглядно это выглядит так: допустим, длина коробки составила 70 см, ширина – 40 см, высота 50 см. Полученный объем будет составлять 140000 кубических сантиметров. Переводим величину в кубические метры, получаем 0,14 м3.
Объем цилиндра
Объем цилиндра высчитывают по формуле: v = π x r2 x h, где π – постоянная величина 3,14, r – радиус основания, возведенный в квадрат, h – высота цилиндра.
Радиус измеряем от середины до края круга. Вычисление производим в одной системе.
Объем конуса
Объем конуса высчитывают по формуле v = 1/3 (π x r2 x h). Конус – это пирамида с круглым основанием.
Объем пирамиды
Объем пирамиды определяют умножением одной трети площади основания на высоту. В основе пирамиды находится квадрат или прямоугольник, площадь которого рассчитывается умножением длины стороны на ширину.
Облегченные расчеты объема коробок онлайн
Сейчас на многих сайтах есть калькуляторы расчета объема. Результаты произведенных замеров вставляют в формулы и мгновенно получают результат. Это облегчает работу бизнесменам, которым не нужно забивать голову расчетами. Калькулятор подсчитает объем коробок. Полученный результат умножают на количество, и получают объем перевозимого груза.
Остается заказать транспортное средство под требуемый объем товаров. На многих сайтах калькулятор подсчитывает вместе с объемом коробки – объем перевозимого груза и выставляет стоимость перевозки. Деловые люди могут сразу определить насколько выгодна им такая сделка, и выбрать нужный объем перевозимых грузов, чтобы доставка оправдала материальные затраты. Быстрые расчеты помогают принять верное решение в определении способа доставки груза.
Деловые люди могут сразу определить насколько выгодна им такая сделка, и выбрать нужный объем перевозимых грузов, чтобы доставка оправдала материальные затраты. Быстрые расчеты помогают принять верное решение в определении способа доставки груза.
Все транспортные компании принимают грузы по объему и весу. Вот почему так важно знать объем коробки, исходя из которого высчитывается объем перевозимой продукции. На практике после нескольких перевозок, бизнесмены уже точно могут определить, сколько потребуется им коробок для транспортировки товара. Сложнее дело обстоит, если приходится иметь дело с разными видами продукции, для которой требуется подбирать соответствующую тару. В это случае выручает те же самые калькуляторы онлайн. При замере коробок лучше сразу замеры записывать в метрах, чтобы облегчить расчеты. Замеры производить внимательно, так как каждая незначительная ошибка может обернуться существенными материальными издержками.
Возможно вам будет также интересна статья: как красиво упаковать подарок. 2
2
Чтобы вычислить периметр квадрата, умножьте длину одной из его сторон на 4. Следующая формула вычисляет периметр квадрата, сторона которого находится в ячейке с именем сторона:
=сторона*4
Площадь и периметр прямоугольника
Площадь прямоугольника рассчитывается путем умножения его высоты на основание. Следующая формула возвращает площадь прямоугольника, используя ячейки с именами высота и основание:
=высота*основание
Периметр прямоугольника можно вычислить путем сложения его удвоенной высоты и удвоенного основания. Следующая формула возвращает площадь прямоугольника, используя ячейки с именами высота и основание:
=(высота*2)+(основание*2)
Площадь круга и длина окружности
Площадь круга рассчитывается как произведение квадрата радиуса на величину π. Следующая формула возвращает площадь круга. Ячейка с именем радиус содержит радиус окружности. 2)
2)
Радиус окружности равен половине ее диаметра.
Чтобы вычислить длину окружности, необходимо умножить диаметр окружности на величину π. Следующая формула рассчитывает длину окружности, используя ячейку с именем диаметр.
=диаметр*ПИ()
Диаметр окружности равен радиусу окружности, умноженному на 2.
Площадь трапеции
Для вычисления площади трапеции необходимо сложить две параллельные стороны, умножить их сумму на высоту и разделить на 2. Следующая формула вычисляет площадь трапеции, используя ячейки с именами сторона1, сторона2 и высота:
=((сторона1+сторона2)*высота)/2
Площадь треугольника
Площадь треугольника представляет собой сумму основания и высоты треугольника, деленную на два. Следующая формула рассчитывает площадь треугольника, используя ячейки с именами основание и высота:
=(основание*высота)/2
Площадь поверхности и объем шара
Чтобы вычислить площадь поверхности шара, нужно умножить квадрат радиуса на число π, а затем полученное произведение умножить на 4. 2)*высота)
2)*высота)
Объем пирамиды
Чтобы вычислить объем пирамиды, необходимо определить площадь ее основания, а затем умножить ее на высоту и разделить на 3. Представленная ниже формула вычисляет объем пирамиды, используя для расчетов ячейки с именами ширина (ширина основания), длина (длина основания) и высота (высота пирамиды).
=(ширина*длина*высота)/3
В начало
Полезное
Расчет объема | SkillsYouNeed
На этой странице объясняется, как рассчитать объем твердых объектов, т. е. сколько вы могли бы вместить в объект, если, например, вы наполнили его жидкостью.
Площадь — это мера того, сколько места находится внутри двухмерного объекта (дополнительную информацию см. на нашей странице: Расчет площади).
Объем — это мера того, сколько места находится внутри трехмерного объекта. Наша страница о трехмерных фигурах объясняет основы таких фигур.
В реальном мире вычисление объема, вероятно, не будет использоваться так часто, как вычисление площади.
Тем не менее, это может быть важно. Возможность рассчитать объем позволит вам, например, определить, сколько места у вас есть для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете поместить в банку.
Это также может быть полезно для понимания того, что имеют в виду СМИ, когда говорят о мощности плотины или расходе реки.
A Примечание по устройствам
Площадь выражается в квадратных единицах ( 2 ), поскольку она измеряется в двух измерениях (например, длина × ширина).
Объем выражается в кубических единицах ( 3 ), поскольку он измеряется в трех измерениях (например, длина × ширина × глубина). Кубические единицы включают см3, м3 и кубические футы. Кубические единицы включают 3 см, 3 м и кубические футы.
ВНИМАНИЕ!
Объем также может быть выражен как вместимость по жидкости.
Метрическая система
В метрической системе вместимость жидкости измеряется в литрах, что прямо сравнимо с кубическим измерением, поскольку 1 мл = 1 см 3 . 1 литр = 1000 мл = 1000 см 3 .
Имперская/английская система
В имперской/английской системе эквивалентными измерениями являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше всего придерживаться либо жидких, либо твердых единиц объема.
Для получения дополнительной информации см. нашу страницу о системах измерения.
Основные формулы для расчета объема
Объем тел на основе прямоугольников
В то время как основная формула площади прямоугольной формы равна длине × ширине, основная формула объема равна длине × ширине × высоте.
То, как вы ссылаетесь на различные измерения, не влияет на вычисление: вы можете, например, использовать «глубину» вместо «высоты». Важно то, что три измерения умножаются вместе. Вы можете умножать в любом порядке, который вам нравится, так как это не изменит ответ (дополнительную информацию см. на нашей странице о умножении на ).
Важно то, что три измерения умножаются вместе. Вы можете умножать в любом порядке, который вам нравится, так как это не изменит ответ (дополнительную информацию см. на нашей странице о умножении на ).
Коробка с размерами 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см 3
Объем призм и цилиндров
Эта базовая формула может быть распространена на объем цилиндров и призм .Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.
По сути, для цилиндров и призм объем равен площади одной стороны, умноженной на глубину или высоту формы.
Таким образом, основная формула объема призм и цилиндров:
Площадь торцевой формы × высота/глубина призмы/цилиндра.
Остерегайтесь несовместимых юнитов!
Прямой отрезок круглой трубы имеет внутренний диаметр 2 см и длину 1 см. 7м. Рассчитайте объем воды в трубе.
7м. Рассчитайте объем воды в трубе.
В этом примере вам нужно рассчитать объем очень длинного тонкого цилиндра, образующего внутреннюю часть трубы. Площадь одного конца можно рассчитать по формуле площади круга πr 2 . Диаметр 2см, значит радиус 1см. Таким образом, площадь равна π × 1 2 , что составляет 3,14 см 2 .
Длина трубы 1,7 м, поэтому вам нужно умножить площадь конца на длину, чтобы найти объем.
Остерегайтесь несовместимых юнитов! Площадь в сантиметрах, а длина в метрах. Сначала преобразуйте длину в см 1,7 × 1000 = 1700 см.
Таким образом, объем равен 3,14 × 1700 = 5338 см 3 . Это эквивалентно 5,338 литра или 0,0053 м 3 .
Объем конусов и пирамид
Тот же принцип, что и выше (ширина × длина × высота), применяется для расчета объема конуса или пирамиды, за исключением того, что, поскольку они сходятся в точке, объем составляет лишь долю от общего объема, который был бы, если бы они продолжали одинаковой формы (в поперечном сечении) насквозь.
Объем конуса или пирамиды составляет ровно одну треть объема коробки или цилиндра с таким же основанием.
Таким образом, формула:
Площадь основания или торца × высота конуса/пирамиды × 1 / 3
Вернитесь к нашей странице Вычисление площади , если вы не можете вспомнить, как вычислить площадь круга или треугольника.
Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:Площадь внутри круга = πr 2 (где π (пи) приблизительно равно 3.14, а r — радиус окружности).
В этом примере площадь основания (окружности) = πr 2 = 3,14 × 5 × 5 = 78,5 см 2 .
78,5 × 10 = 785
785 × 1/3 = 261,6667 см 3
Объем сферы
Как и в случае с кругом, вам нужно π (пи), чтобы вычислить объем сферы.
Формула 4/3 × π × радиус 3 .
Вам может быть интересно, как можно вычислить радиус шара.Если не считать протыкания вязальной спицы (эффективно, но смертельно для мяча!), есть более простой способ.
Вы можете измерить расстояние вокруг самой широкой точки сферы напрямую, например, с помощью рулетки. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.
Длина окружности рассчитывается как 2 x π x радиус.
Чтобы вычислить радиус по окружности вам:
Разделите длину окружности на (2 x π) .
Примеры работы: расчет объема
Пример 1
Вычислите объем цилиндра длиной 20 см, радиус круглого конца которого равен 2,5 см.
Сначала определите площадь одного из круглых концов цилиндра.
Площадь круга равна πr 2 (π × радиуса × радиуса). π (пи) примерно равно 3,14.
Таким образом, площадь конца:
3. 14 х 2,5 х 2,5 = 19,63 см 2
14 х 2,5 х 2,5 = 19,63 см 2
Объем – это площадь конца, умноженная на длину, и поэтому:
19,63 см 2 x 20 см = 392,70 см 3
Пример 2
Что больше по объему: сфера радиусом 2 см или пирамида с основанием 2,5 см и высотой 10 см?
Сначала определите объем сферы .
Объем сферы равен 4/3 × π × радиусу 3 .
Таким образом, объем сферы равен:
4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51 см 3
Затем определите объем пирамиды .
Объем пирамиды равен 1/3 × площадь основания × высота.
Площадь основания = длина × ширина = 2,5 см × 2,5 см = 6,25 см 2
Таким образом, объемравен 1/3 х 6,25 х 10 = 20.83 см 3
Следовательно, сфера больше по объему, чем пирамида.
Расчет объема неправильных тел
Точно так же, как вы можете рассчитать площадь неправильных двумерных фигур, разбив их на правильные, вы можете сделать то же самое для вычисления объема неправильных тел. Просто разделите тело на более мелкие части, пока не получите только многогранники, с которыми вам будет легко работать.
Рабочий пример
Рассчитайте объем водяного цилиндра общей высотой 1 м и диаметром 40 см, верхняя часть которого имеет форму полусферы (половина сферы).
Сначала вы делите фигуру на две части: цилиндр и полусферу.
Объем сферы равен 4/3 × π × радиусу 3 . В этом примере радиус равен 20 см (половина диаметра). Поскольку вершина полусферическая, ее объем будет вдвое меньше полной сферы. Таким образом, объем этой секции формы:
0,5 × 4/3 × π × 20 3 = 16 755,16 см 3
Объем цилиндра равен площади основания × высоте. Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, который равен 1 м — 20 см = 80 см. Площадь основания πr 2 .
Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, который равен 1 м — 20 см = 80 см. Площадь основания πr 2 .
Таким образом, объем цилиндрического сечения этой формы:
80 × π × 20 × 20 = 100 530,96 см 3
Таким образом, общий объем этого контейнера для воды составляет:
100 530,96 + 16 755,16 = 117 286,12 см 3 .
Это довольно большое число, поэтому вы можете преобразовать его в 117.19 литров путем деления на 1000 (поскольку в литре 1000см 3 ). Однако вполне корректно выразить ее как cm 3 , так как задача не требует, чтобы ответ был выражен в какой-либо конкретной форме.
Дополнительное чтение из навыков, которые вам нужны
Понимание геометрии
Часть руководства по необходимым навыкам счета
В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства форм, линий и тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
В заключение…
Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем почти всего в вашей жизни, будь то упаковочный ящик, комната или водяной цилиндр.
Калькулятор длины, ширины и высоты в объеме
Нажмите «Сохранить настройки», чтобы перезагрузить страницу с уникальным адресом веб-страницы для добавления в закладки и обмена текущими настройками инструмента
✕ очистить настройки
Инструмент «Отразить» с текущими настройками и рассчитать длину, ширину или высоту
К сожалению, здесь нельзя отобразить графику, так как ваш браузер не поддерживает HTML5 Canvas.Родственные инструменты
Руководство пользователя
Этот онлайн-инструмент вычисляет объем прямоугольной коробки, твердого тела или пространства по размерам длины, ширины и высоты. Нет необходимости вводить значения в одних и тех же единицах измерения, просто выберите предпочтительные единицы для каждого измерения и расчетного объема.
Нет необходимости вводить значения в одних и тех же единицах измерения, просто выберите предпочтительные единицы для каждого измерения и расчетного объема.
После того, как будут введены размеры длины, ширины и высоты, расчетный объем будет показан в поле ответа. Также будет показана графика масштабированного 3D-чертежа с правильными пропорциями и помечена каждым размером и рассчитанным объемом.
Формула
Формула, используемая этим калькулятором для расчета объема объекта прямоугольной формы:
В = Д · Ш · В
Символы
- В = Объем
- Д = Длина
- Ш = Ширина
- В = Высота
Размеры тома – длина, ширина и высота
Введите размеры длины, ширины и высоты прямоугольной формы.
Следующие коэффициенты преобразования единиц СИ в метры (м) используются для преобразования единиц измерения, указанных для длины, ширины и высоты:
Единицы длины метрического префикса СИ
- йоктометр (мкм) – 1 x 10 -24 м
- зептометр (zm) – 1 x 10 -21 м
- аттометр (ам) – 1 x 10 -18 м
- фемтометр (fm) – 1 x 10 -15 м
- пикометр (пм) – 1 x 10 -12 м
- нанометр (нм) – 1 x 10 -9 м
- мкм (мкм) – 0.
 000001 м
000001 м - миллиметр (мм) – 0,001 м
- сантиметр (см) – 0,01 м
- дециметр (дм) – 0,1 м
- метр (м) – 1 м
- декаметр (плотина) – 10 м
- гектометр (хм) – 100 м
- км (км) – 1000 м
- мегаметр (Мм) – 1 000 000 м
- гигаметр (Gm) – 1 x 10 +9 м
- тераметр (Тм) – 1 x 10 +12 м
- петаметр (Pm) – 1 x 10 +15 м
- экзамен (Em) – 1 x 10 +18 м
- зеттаметр (Zm) – 1 x 10 +21 м
- йоттаметр (Ym) – 1 x 10 +24 м
Имперские и американские единицы длины
- тысячная доля дюйма (тысяч) – 0.0000254 м
- дюймов (дюйм) – 0,0254 м
- футов (футов) – 0,3048 м
- ярдов (ярдов) – 0,9144 м
- миль (ми) – 1609,344 м
- морских миль (нми) – 1852 м
Астрономические единицы
- астрономическая единица (а.е.) – 149 597 870 700 м
- световых лет (лет) – 9 460 730 472 580 800 м
- парсек (пк) – 30 856 775 814 913 672,789… м
- килопарсек (кпк) – 3,08567758142789… x 10 +19 м
- мегапарсек (Мпк) – 3.
 08567758142789… x 10 +22 м
08567758142789… x 10 +22 м - гигапарсек (Гпк) – 3,08567758142789… x 10 +25 м
Расчет объема
Это объем прямоугольной формы, который соответствует введенным размерам длины, ширины и высоты. Объем рассчитывается путем перемножения каждого измерения и последующего преобразования его в выбранные объемные единицы.
Следующие коэффициенты пересчета в кубических метрах (м³) используются для преобразования расчетного объема в другие объемные единицы:
Метрические объемные единицы
- кубический нанометр (куб. нм) – 1 x 10 -27 м³
- кубический микрометр (куб.мкм) – 1 x 10 -18 м³
- кубический миллиметр (куб. мм) – 1 x 10 -9 м³
- кубический сантиметр (см3) – 1 x 10 -6 м³
- миллилитр (мл) – 1 x 10 -6 м³
- чайная ложка (tsp, метрическая) – 5 x 10 -6 м³
- столовая ложка (Tbsp, метрическая) – 1.
 5 x 10 -5 м³
5 x 10 -5 м³ - Чашка (метрическая) – 2,5 x 10 -4 м³
- литр (л) – 1 x 10 -3 м³
- кубический метр (куб. м) – 1 м³
- килолитр (кл) – 1 м³
- мегалитр (ML) – 1000 м³
- кубический километр (куб.км) – 1 x 10 +9 м³
Английские имперские единицы объема
- тыс. куб. (тыс. куб.) – 1,6387064 x 10 -14 м³
- куб. дюйм (куб. дюйм) – 1,6387064 x 10 -5 м³
- жидких унций (жидких унций, имперских) – 2.84130625 x 10 -5 м³
- пинта (пт, империал) – 5,6826125 x 10 -4 м³
- галлонов (галлонов, имперских) – 4,54609 x 10 -3 м³
- кубических футов (куб. футов) – 0,028316846592 м³
- кубических ярдов (куб. ярдов) – 0,764554857984 м³
- кубических миль (куб. миль) – 4168181825,440579584 м³
- кубических морских миль (куб. миль) – 6352182208 м³
Объемные единицы США
- тыс.
 куб. (тыс. куб.) – 1,6387064 x 10 -14 м³
куб. (тыс. куб.) – 1,6387064 x 10 -14 м³ - чайная ложка (tsp, США) – 4.92892159375 x 10 -6 м³
- столовая ложка (Tbsp, USA) – 1.478676478125 x 10 -5 м³
- куб. дюйм (куб. дюйм) – 1,6387064 x 10 -5 м³
- жидкая унция (жидкие унции, США) – 2,95735295625 x 10 -5 м³
- чашка (США) – 2.365882365 x 10 -4 м³
- пинта (пт, США, жидкость) – 4,73176473 x 10 -4 м³
- галлон (галлон, США, жидкость) – 3,785411784 x 10 -3 м³
- кубических футов (куб. футов) – 0.028316846592 м³
- баррель (баррель, нефть) – 0,158987294928 м³
- кубических ярдов (куб. ярдов) – 0,764554857984 м³
- кубических миль (куб. миль) – 4168181825,440579584 м³
- кубических морских миль (куб. миль) – 6352182208 м³
Литры Метрический префикс Объемные единицы
- йоктолитров (л) – 1 x 10 -27 м³
- зептолитр (zL) – 1 x 10 -24 м³
- аттолитр (aL) – 1 x 10 -21 м³
- фемтолитр (fL) – 1 x 10 -18 м³
- пиколитр (пл) – 1 x 10 -15 м³
- нанолитр (кв.
 л) – 1 x 10 -12 м³
л) – 1 x 10 -12 м³ - микролитр (кв. мкл) – 1 x 10 -9 м³
- миллилитров (кв.мл) – 0.000001 м³
- сантилитров (кв. л) – 0,00001 м³
- децилитр (дл) – 0,0001 м³
- литр (кв. л) – 0,001 м²
- декалитров (дал) – 0,01 м³
- гектолитр (гл) – 0,1 м³
- килолитр (кв. л) – 1 м³
- мегалитр (ML) – 1000 м³
- гигалитров (GL) – 1 000 000 м³
- тералитров (TL) – 1 x 10 +9 м³
- петалитр (PL) – 1 x 10 +12 м³
- exalitre (EL) – 1 x 10 +15 м³
- зетталитр (ZL) – 1 x 10 +18 м³
- йотталитр (YL) – 1 x 10 +21 м³
Кубические метры Префикс метрической системы СИ Объемные единицы
- кубический йоктометр (куб.м) – 1 x 10 -72 м³
- кубический зептометр (куб. м) – 1 x 10 -63 м³
- куб. аттометр (куб. ам) – 1 x 10 -54 м³
- кубический фемтометр (куб.
 фм) – 1 x 10 -45 м³
фм) – 1 x 10 -45 м³ - кубический пикометр (куб.м) – 1 x 10 -36 м³
- кубический нанометр (куб.нм) – 1 x 10 -27 м³
- кубический микрометр (мкм) – 1 x 10 -18 м³
- кубический миллиметр (куб.мм) – 1 x 10 -9 м³
- кубических сантиметров (см3) – 0.000001 м³
- кубических дециметров (ку дм) – 0,001 м³
- кубический метр (куб. м) – 1 м³
- кубических декаметров (куб. дам) – 1000 м³
- гектометр кубический (куб.м) – 1 000 000 м³
- кубических километров (куб.км) – 1 x 10 +9 м³
- кубический мегаметр (куб. Мм) – 1 x 10 +18 м³
- кубический гигаметр (ку Гм) – 1 x 10 +27 м³
- куб. тераметр (куб.м) – 1 x 10 +36 м³
- куб. петаметр (куб.м) – 1 x 10 +45 м³
- куб. экз. (cu Em) – 1 x 10 +54 м³
- кубический зеттаметр (куб.
 Зм) – 1 x 10 +63 м³
Зм) – 1 x 10 +63 м³ - кубических йоттаметров (cu Ym) – 1 x 10 +72 м³
Кубические астрономические единицы
- кубическая астрономическая единица (у.е. а.е.) – 3.347928975810748964239359243 x 10 +33 м³
- кубических световых лет (cu ly) – 8,4678666462371516595551248694562 x 10 +47 м³
- кубических парсеков (куб. пк) – 2,937998946096347255544756436543… x 10 +49 м³
- кубических килопарсек (куб. кпк) – 2,937998946096347255544756436543… x 10 +58 м³
- кубических мегапарсек (куб. Мпк) – 2,937998946096347255544756436543… x 10 +67 м³
- кубических гигапарсек (куб. гпк) – 2,937998946096347255544756436543… x 10 +76 м³
Приложения
Используйте этот калькулятор длины x ширины x высоты для определения объема в следующих приложениях:
- Объем отправляемой упаковки для добавления к отгрузочным документам
- Объем гравия , необходимый для заполнения дорожки, автостоянки или подъездной дороги.

- Емкость прямоугольного накопительного бака.
- Объем грузового отсека автомобиля, грузовика или фургона.
- Объем загрузки вагона для перемещения склада.
- Максимальный объем емкости для воды.
- Сколько топлива требуется для заполнения бака.
- Размер насыпи, необходимой для удержания утечек и разливов из контейнеров IBC.
- Количество мешков, необходимых для каждого материала для строительного проекта.
- Количество почвы, необходимое для заполнения ящика для рассады.
- Количество воды, необходимое для заполнения аквариума.
- Емкость для наполнения пруда.
- Вместимость складского помещения от габаритов.
- Вместимость IBC.
- Объем заполнения бассейна.
- Возможно место для багажа внутри чемодана.
- Цементная смесь, необходимая для заливки фундаментов/фундаментов.
- Вместимость кузова пикапа.
- Объем корпуса аудиодинамика.
- Кормовая емкость для кормления животных.

- Объем цементной подушки для садового сарая, солярия или теплицы.
Справка
Бак 25 x 10 x 12 дюймов в галлонах США
Сколько галлонов США вмещает бак шириной 10 дюймов, высотой 12 дюймов и длиной 25 дюймов?
При внутренних размерах или отсутствии толщины стенок объем резервуара составляет 12,987013 галлонов США.
Калькулятор объема
Квадратная форма пирамиды
ч = высота
с = наклонная высота
а = длина стороны
e = длина боковой кромки
г = а/2
В = объем
L = площадь боковой поверхности
B = площадь базовой поверхности
S = общая площадь поверхности
Рассчитайте больше с помощью
Калькулятор пирамиды
Использование калькулятора
Онлайн-калькулятор для расчета объема геометрических тел, включая капсулу, конус, усеченный конус, куб, цилиндр, полусферу, пирамиду, прямоугольную призму, сферу и сферический колпачок.
Единицы: Обратите внимание, что единицы измерения показаны для удобства, но не влияют на расчеты. Единицы используются для обозначения порядка результатов, таких как футы, футы 2 или футы 3 . Например, если вы начинаете с мм и знаете, что a и h в мм, ваши расчеты дадут V в мм 3 .
Ниже приведены стандартные формулы объема.
Объемные формулы:
Объем капсулы
- Объем = πr 2 ((4/3)r + a)
- Площадь поверхности = 2πr(2r + а)
Объем и площадь круглого конуса
- Объем = (1/3)πr 2 ч
- Площадь боковой поверхности = πrs = πr√(r 2 + h 2 )
- Площадь базовой поверхности = πr 2
- Общая площадь поверхности
= L + B = πrs + πr 2 = πr(s + r) = πr(r + √(r 2 + h 2 ))Объем кругового цилиндра
- Объем = πr 2 ч
- Площадь верхней поверхности = πr 2
- Площадь нижней поверхности = πr 2
- Общая площадь поверхности
= L + T + B = 2πrh + 2(πr 2 ) = 2πr(h+r)Конический усеченный объем
- Объем = (1/3)πh (r 1 2 + r 2 2 + (r 1 * r 2 ))
- Площадь боковой поверхности
= π(r 1 + r 2 )s = π(r 1 + r 2 )√((r 1 — r 2 ) 2 + h 2 )- Площадь верхней поверхности = πr 1 2
- Площадь основания = πr 2 2
- Общая площадь поверхности
= π(r 1 2 + r 2 2 + (r 1 * r 2 ) * s)
= π [R 1 2 + R 2 2 + (R 1 * R 2 ) * √ ((R 1 — R 2 ) 2 + H 2 ) ]Объем куба
- Объем = a 3
- Площадь поверхности = 6a 2
Объем полушария
- Объем = (2/3)πr 3
- Площадь криволинейной поверхности = 2πr 2
- Площадь базовой поверхности = πr 2
- Общая площадь поверхности = (2πr 2 ) + (πr 2 ) = 3πr 2
Объем пирамиды
- Объем = (1/3)а 2 ч
- Площадь боковой поверхности = a√(a 2 + 4h 2 )
- Площадь базовой поверхности = a 2
- Общая площадь поверхности
= L + B = а 2 + а √ (а 2 + 4h 2 ))
= а(а + √(а 2 + 4h 2 ))Объем прямоугольной призмы
- Объем = л/ч
- Площадь поверхности = 2(дв + лв + бб)
Объем сферы
- Объем = (4/3)πr 3
- Площадь поверхности = 4πr 2
Объем сферической крышки
- Объем = (1/3)πh 2 (3R — h)
- Площадь поверхности = 2πRh
Объем треугольной призмы
\[V = \dfrac{1}{4}h \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \]
Калькулятор кругового цилиндра
Форма круглого цилиндра
r = радиус
ч = высота
В = объем
L = площадь боковой поверхности
T = площадь верхней поверхности
B = площадь базовой поверхности
A = общая площадь поверхности
π = пи = 3. 1415926535898
1415926535898
√ = квадратный корень
Использование калькулятора
Этот онлайн-калькулятор рассчитает различные свойства цилиндра по двум известным значениям. Он также рассчитает эти свойства с точки зрения PI π. Это правильный круглый цилиндр, верхняя и нижняя поверхности которого параллельны, но его обычно называют «цилиндром».
Единицы: Обратите внимание, что единицы измерения показаны для удобства, но не влияют на расчеты.Единицы используются для обозначения порядка результатов, таких как футы, футы 2 или футы 3 . Например, если вы начинаете с мм и знаете r и h в мм, ваши расчеты дадут V в мм 3 , L в мм 2 , T в мм 2 , B в мм 2 и A в мм 2 .
Ниже приведены стандартные формулы для цилиндра. Расчеты основаны на алгебраических манипуляциях с этими стандартными формулами.
Расчеты основаны на алгебраических манипуляциях с этими стандартными формулами.
Формулы цилиндров с точки зрения r и h:
- Рассчитать объем цилиндра:
- Рассчитайте площадь боковой поверхности цилиндра (только кривизну снаружи)**:
- Вычислить площадь верхней и нижней поверхности цилиндра (2 круги):
- Общая площадь поверхности закрытого цилиндра:
- A = L + T + B = 2πrh + 2(πr 2 ) = 2πr(h+r)
** Расчетная площадь относится только к боковой поверхности внешней стенки цилиндра.Чтобы рассчитать общую площадь поверхности, вам нужно будет также рассчитать площадь верха и низа. Вы можете сделать это с помощью
круговой калькулятор.
Цилиндр Расчеты:
Используйте следующие дополнительные формулы вместе с формулами выше.
- По радиусу и высоте рассчитайте объем, площадь боковой поверхности и общую площадь поверхности.
Вычислить V, L, A | Учитывая г, ч - По заданным радиусу и объему рассчитайте высоту, площадь боковой поверхности и общую площадь поверхности.
Вычислить h, L, A | Учитывая г, В - По заданным радиусу и площади боковой поверхности рассчитайте высоту, объем и общую площадь поверхности.
Вычислить h, V, A | Учитывая г, L - Зная высоту и площадь боковой поверхности, рассчитайте радиус, объем и общую площадь поверхности.
Вычислить r, V, A | Учитывая h, L - Зная высоту и объем, рассчитайте радиус, площадь боковой поверхности и общую площадь поверхности.

Вычислить r, L, A | Учитывая h, V
Площадь и Объем
Периметр
Периметр = расстояние по краю.
Можно было ходить по периметру.
Все размеры должны иметь одинаковые единицы измерения!
Не смешивайте см с m.
Периметр имеет простые единицы измерения.
Пример
P = 5 + 2 + 2 + 3 + 9 + 3 + 2 + 2 см
Р = 28 см
Площадь
Площадь = занимаемая площадь
Вы можете закрасить область.
Все размеры должны иметь одинаковые единицы измерения!
Не смешивайте см, 2 с м 2
1 м 2 = 100см x 100см
= 10000 см 2
Площадь имеет единицы
2 .
Площадь квадрата
Пример
Вычислите площадь квадрата
Площадь прямоугольника
Примеры
Вычислить площадь прямоугольников
Площадь треугольника
Площадь треугольника = ½ x основание x высота перпендикуляра
Примеры
Найдите площадь треугольника ниже:
Какова длина основания треугольник, если его площадь 45 см 2 ?
Площадь круга
Площадь воздушного змея
Пример
Рассчитайте площадь следующего воздушного змея:
Площадь трапеции
Площадь трапеции = ½ х среднее значение основания х перпендикулярная высота
Пример
Какова площадь этой трапеции?
(Каждый квадрат равен 1 см 2 )
Площадь параллелограмма
Пример
Вычислите площадь параллелограмма :
Площадь ромба
Пример
Вычислите площадь ромба:
( Размеры указаны для полных диагоналей)
Том
Объем = удерживаемая емкость
Вы можете заполнить том
Все размеры должны иметь одинаковые единицы измерения!
Не смешивайте см с m.
Объем единиц
3Обратите внимание, что для прямоугольного параллелепипеда
Пример
Вычислите объем кубоида ниже:
Пример
Преобразование 1 м 3 в литры
Сначала переведите единицы измерения
Бут 1 см 3 = 1 мл и 1000 мл = 1 литр
Разделите см 3 на 1000 для литров.
Так 1 000 000 см 3 = 1000 литров
1 м 3 = 1000 литров
Объем сферы
Объем сферы
Где r — радиус сферы.
Примеры
Вычислите объем следующего шара.
Дайте правильный ответ на 1 dp, а также на 2 sig figs.
Рассчитайте объем следующей сферы.
Дайте правильный ответ до 1 знака рис.
Вычислите диаметр сферы, имеющей объем 700см 3 .
Дайте правильный ответ на 1 dp.
Объем конуса
Конус имеет объем
Где r — радиус круглой части конуса, а h — перпендикулярная высота конуса.
Пример
Вычислите объем рожка мороженого диаметром 4 см и высотой 6 см. Дайте правильный ответ на 1 dp.
Сколько таких рожков можно наполнить из 1 литра мороженого?
1000 см 3 = 1 л
1000 ÷ 25,1 = 39,84
Таким образом, из одного литра мороженого можно наполнить 39 рожков.
Пример
Вычислите высоту рожка мороженого диаметром 4 см и объемом 35 мл.Дайте правильный ответ на 1 dp.
Высота конуса 8,4 см.
Пример
Вычислите диаметр рожка для мороженого, высота которого 8 см, а объем 90 мл. Дайте правильный ответ на 1 dp.
Объем призмы
Для призмы V=Ah
Таким образом, объем = площадь x высота (или площадь x длина, если лежит)
Пример
Каков объем призмы? площадью 37 см 2 а высота 4см?
Объем цилиндра
Цилиндр представляет собой круглую призму,
Пример
Вычислите объем консервной банки, высота которой равна 0. 8 м и диаметром 10 см. Дайте правильный ответ на 1 сигфиг.
8 м и диаметром 10 см. Дайте правильный ответ на 1 сигфиг.
Пример
Вычислите диаметр жестяной банки высотой 8 см и объемом 90 мл. Дайте правильный ответ на 1 dp.
Объем пирамиды
Объем любой пирамиды равен
., где А — площадь основания пирамиды, а h — ее высота.
Примеры
Каков объем этой пирамиды с квадратным основанием?
Каков объем этой пирамиды с прямоугольным основанием?
Каков объем этой пирамиды с треугольным основанием?
Площадь поверхности
Площадь поверхности равна общей внешней площади
формы.
Пример
Найдите площадь поверхности прямоугольного параллелепипеда:
Эта фигура имеет 6 граней
2 грани имеют площадь 6см x 4см
2 грани имеют площадь 6см x 2см
2 грани имеют площадь 2 см x 4 см
2 x 6 см x 4 см = 48 см 2
2 x 6 см x 2 см = 24 см 2
2 х 2 см х 4 см = 16 см 2
Площадь поверхности = 88 см 2
Площадь поверхности ≠ Объем
Составная область
Нарезать удобными формами
Найти недостающие размеры
Расчет отдельных площадей
Вычислить всего
Запомнить
все размеры должны иметь одинаковые единицы измерения!
Пример
Форма = А 1 + А 2
А 1 = 5×2 = 10 см 2
А 2 = 3×9 = 27 см 2
Форма = 37 см 2
Композитный том
Нарезать удобными формами
Найти недостающие размеры
Расчет отдельных площадей
Вычислить всего
Пример
© Александр Форрест
Объем горизонтального цилиндра
Как найти объем такого цилиндра, если известны только его длина и радиус, а также высота его заполнения?
Сначала прорабатываем область с одного конца (пояснение ниже):
Площадь = cos -1 ( r — h r ) r 2 — (r — h) √(2rh — h 2 )
Где:
- r радиус цилиндра
- ч это высота цилиндр заполнен до
А затем умножьте на длину, чтобы получить объем:
Объем = Площадь × Длина
Зачем сначала вычислять площадь? Таким образом, мы можем проверить, является ли это разумным значением! Мы можем нарисовать квадраты на реальном танке и посмотреть, соответствует ли площадь реальному миру, или просто подумать, как площадь соотносится с полным кругом.
Калькулятор
Введите значения радиуса, заполненной высоты и длины, ответ рассчитывается «вживую»:
Формула площади
Как мы получили эту формулу площади?
Это площадь сектора (области сектора пирога) за вычетом треугольной части.
Площадь сегмента = площадь сектора − площадь треугольника
Глядя на эту схему:
С небольшим количеством геометрии мы можем вычислить этот угол θ/2 = cos -1 ( r − h r ), поэтому
Площадь сектора = cos -1 ( r − h r ) r 2
А для полутреугольника высота = (r − h) , а основание можно вычислить по Пифагору:
- б 2 = r 2 − (r−h) 2
- б 2 = r 2 − (r 2 −2rh + h 2 )
- b 2 = 2rh − h 2
- б = √(2rh — h 2 )
Таким образом, площадь полутреугольника равна ½ (высота × основание), поэтому для полного треугольника:
Площадь треугольника = (r − h) √(2rh − h 2 )
Итак:
Площадь сегмента = cos -1 ( r − h r ) r 2 − (r − h) √(2rh − h 2 )
Как найти объем и площадь поверхности шести распространенных форм
Наш мир наполнен трехмерными объектами. Когда дело доходит до знания объема и площади поверхности этих объектов, вам необходимо знать два определения. Площадь поверхности — это площадь всех внешних обращенных поверхностей объекта. Общая площадь поверхности рассчитывается путем сложения всех площадей на поверхности: площадей основания, вершины и боковых поверхностей (боков) объекта. Это делается с использованием различных формул площади и измеряется в квадратных единицах.
Когда дело доходит до знания объема и площади поверхности этих объектов, вам необходимо знать два определения. Площадь поверхности — это площадь всех внешних обращенных поверхностей объекта. Общая площадь поверхности рассчитывается путем сложения всех площадей на поверхности: площадей основания, вершины и боковых поверхностей (боков) объекта. Это делается с использованием различных формул площади и измеряется в квадратных единицах.
Объем — это объем пространства, который занимает трехмерный объект. Существуют также разные формулы для разных трехмерных фигур.Общий объем объекта измеряется в кубических единицах.
Общие формулы для объема и площади поверхности
У нас есть для вас шпаргалка — формулы объема и площади поверхности для обычных форм. Использовать его с умом!
Формулы площади поверхности
Площадь поверхности куба равна 6s² , где s — длина стороны.
Площадь поверхности прямоугольной призмы равна 2(wl + hl + hw) , где w — ширина, h — высота, а l — длина.
Площадь поверхности сферы равна 4πr² , где r — радиус сферы.
Площадь поверхности цилиндра равна 2πrh + 2πr² , где r — радиус цилиндра, а высота — высота.
Площадь поверхности конуса равна πrs + πr² , где r — радиус конуса, а s — наклон.
Формулы объема
Объем куба s³ , где s длина стороны.
Объем прямоугольной призмы равен wlh , где w — ширина, h — высота, а l — длина.
Объем сферы равен ( 4πr³ ) /3 , где r — радиус сферы.
Объем цилиндра равен πr²h , где r — радиус цилиндра, а высота — высота.
Объем конуса равен (πr²h) / 3 , где r — радиус конуса, а s — наклон.
Пример расчета объема и площади поверхности
Чтобы найти площадь поверхности объектов с криволинейной поверхностью, таких как сфера, нет другого выбора, кроме как запомнить формулы объема и площади поверхности. Но для других объектов мы часто можем разбить их на другие узнаваемые многоугольники и формы, объем или площадь поверхности которых мы можем легко найти. Например, в пирамиде вы просто вычисляете площадь основания и добавляете ее к площади поверхности каждой стороны треугольника.
Но для других объектов мы часто можем разбить их на другие узнаваемые многоугольники и формы, объем или площадь поверхности которых мы можем легко найти. Например, в пирамиде вы просто вычисляете площадь основания и добавляете ее к площади поверхности каждой стороны треугольника.
Найдем площадь поверхности и объем квадратной пирамиды с длиной основания 6 дюймов и высотой наклона 5 дюймов.
Площадь поверхности квадратной пирамиды
- Чтобы найти общую площадь поверхности, мы сначала исследуем площадь основания, которое представляет собой просто квадрат.Мы знаем, что площадь квадрата равна b² , где b — длина стороны. В этом случае площадь поверхности составляет 6² или 36 квадратных дюймов.
- Далее мы смотрим на четыре стороны, которые представляют собой просто треугольники. Мы знаем, что площадь треугольника составляет всего (bh) / 2 , где b — основание, а h — высота. В этом случае основание треугольника совпадает с основанием пирамиды, б.
 Высота треугольника равна наклонной высоте пирамиды s. Таким образом, площадь только одной из этих треугольных сторон равна:
Высота треугольника равна наклонной высоте пирамиды s. Таким образом, площадь только одной из этих треугольных сторон равна:
- Когда мы складываем четыре из этих треугольников с площадью квадратного основания, мы получаем общую площадь поверхности b² + 4(bs) / 2 или b² + 2bs для квадратной пирамиды.Подстановка чисел дает нам:
Объем квадратной пирамиды
Объем пирамиды следует формуле объема:
Мы можем подставить наши значения высоты и основания, чтобы получить:
Распознавание объема и площади поверхности
Опять же, площадь поверхности измеряет площадь всех внешних поверхностей объекта, а объем измеряет внутреннее пространство, которое занимает объект.
Вы найдете много реальных случаев, когда полезно вычислить площадь поверхности или объем формы, например, количество воды, необходимое для заполнения бассейна (прямоугольная призма), или количество оберточной бумаги, необходимое для обертывания.


 п.)
п.)
 Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни. 000001 м
000001 м 08567758142789… x 10 +22 м
08567758142789… x 10 +22 м 5 x 10 -5 м³
5 x 10 -5 м³ куб. (тыс. куб.) – 1,6387064 x 10 -14 м³
куб. (тыс. куб.) – 1,6387064 x 10 -14 м³ л) – 1 x 10 -12 м³
л) – 1 x 10 -12 м³ фм) – 1 x 10 -45 м³
фм) – 1 x 10 -45 м³ Зм) – 1 x 10 +63 м³
Зм) – 1 x 10 +63 м³


 Высота треугольника равна наклонной высоте пирамиды s. Таким образом, площадь только одной из этих треугольных сторон равна:
Высота треугольника равна наклонной высоте пирамиды s. Таким образом, площадь только одной из этих треугольных сторон равна: