Площадь треугольника. Онлайн-калькулятор
Онлайн-калькулятор для расчета площади треугольника поможет Вам найти площадь треугольника несколькими способами в зависимости от известных данных. Наш калькулятор не просто рассчитает площадь треугольника, но и покажет подробное решение, которое будет показано под калькулятором. Поэтому данный калькулятор удобно использовать не только для быстрых расчетов, но и для проверки своих вычислений. С помощью данного калькулятора вы сможете найти площадь треугольника по следующим формулам: через основание и высоту, через две стороны и угол, по трем сторонам (формула Герона), через радиус вписанной окружности, через радиус описанной окружности.

Выберите способ расчета площади:
через основание и высоту через две стороны и угол по трем сторонам (формула Герона) через радиус вписанной окружности через радиус описанной окружностиТреугольник – это геометрическая фигура, которая образована тремя отрезками. Эти отрезки называются сторонами треугольниками, а точки соединения отрезков – вершинами треугольника. В зависимости от соотношения сторон треугольники бывают нескольких видов: равнобедренный треугольник (две стороный треугольника равны между собой, эти стороны называются боковыми сторонами, а третья сторона называется основанием треугольника), равносторонний треугольник (у треугольника все три стороны равны), прямоугольный треугольник (один угол треугольника прямой).
Как найти площадь треугольника?
Найти площадь треугольника очень просто, достаточно воспользоваться нашим калькулятором или рассчитать самостоятельно, воспользовавшись формулой площади треугольника. В зависимости от того, какие данные известны, для расчета площади треугольника использует несколько способов:
1) через основание и высоту
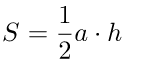 a – основание треугольника,
a – основание треугольника,h – высота треугольника.
2) через две стороны и угол
 a, b – стороны треугольника,
a, b – стороны треугольника,α – угол между сторонами.
3) По трем сторонам. Формула Герона.
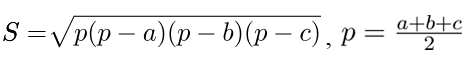 a, b, с – стороны треугольника,
a, b, с – стороны треугольника,p – полупериметр треугольника.
4) Через радиус вписанной окружности.
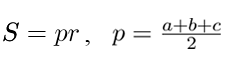
p – полупериметр треугольника,
r – радиус вписанной окружности.
5) Через радиус описанной окружности.
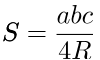 a, b, с – стороны треугольника,
a, b, с – стороны треугольника,R – радиус описанной окружности.
Вы всегда сможете проверить правильность расчета площади треугольника с помощью нашего калькулятора.
Как найти площадь треугольника — Лайфхакер
Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.
Как найти площадь любого треугольника
Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.
Зная сторону и высоту
- Умножьте сторону треугольника на высоту, проведённую к этой стороне.
- Поделите результат на два.
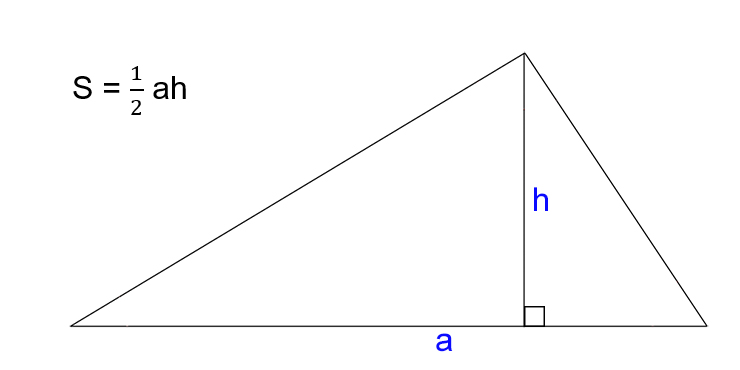
- S — искомая площадь треугольника.
- a — сторона треугольника.
- h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.
Зная две стороны и угол между ними
- Посчитайте произведение двух известных сторон треугольника.
- Найдите синус угла между выбранными сторонами.
- Перемножьте полученные числа.
- Поделите результат на два.
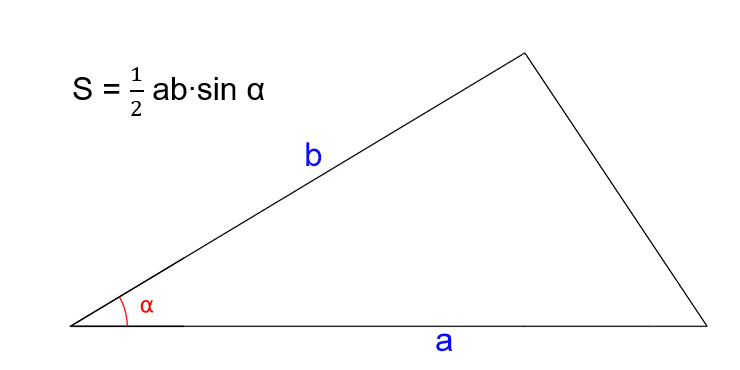
- S — искомая площадь треугольника.
- a и b — стороны треугольника.
- α — угол между сторонами a и b.
Сейчас читают
🔥
Зная три стороны (формула Герона)
- Посчитайте разности полупериметра треугольника и каждой из его сторон.
- Найдите произведение полученных чисел.
- Умножьте результат на полупериметр.
- Найдите корень из полученного числа.
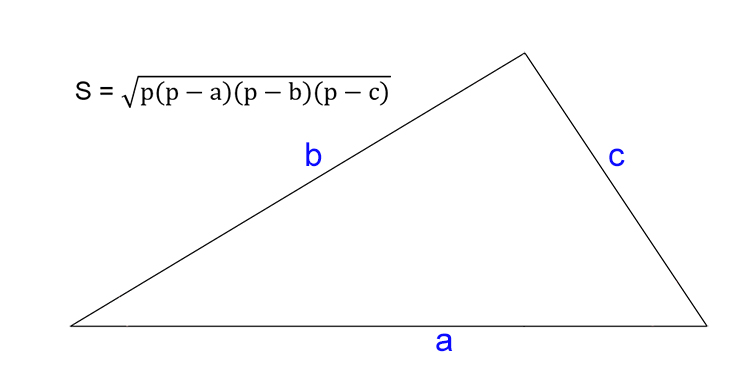
- S — искомая площадь треугольника.
- a, b, c — стороны треугольника.
- p — полупериметр (равен половине от суммы всех сторон треугольника).
Зная три стороны и радиус описанной окружности
- Найдите произведение всех сторон треугольника.
- Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.
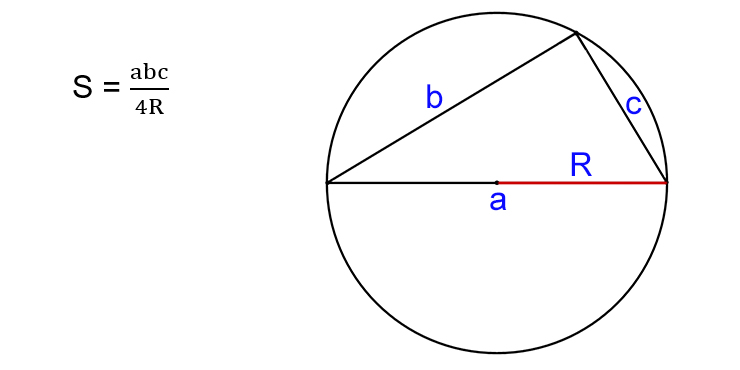
- S — искомая площадь треугольника.
- R — радиус описанной окружности.
- a, b, c — стороны треугольника.
Зная радиус вписанной окружности и полупериметр
Умножьте радиус окружности, вписанной в треугольник, на полупериметр.
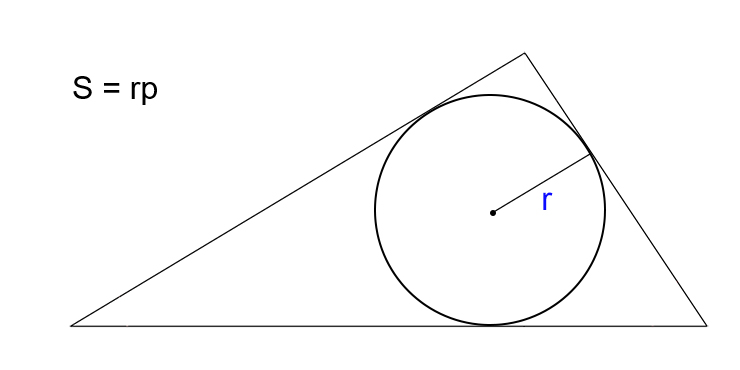
- S — искомая площадь треугольника.
- r — радиус вписанной окружности.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Как найти площадь прямоугольного треугольника
- Посчитайте произведение катетов треугольника.
- Поделите результат на два.
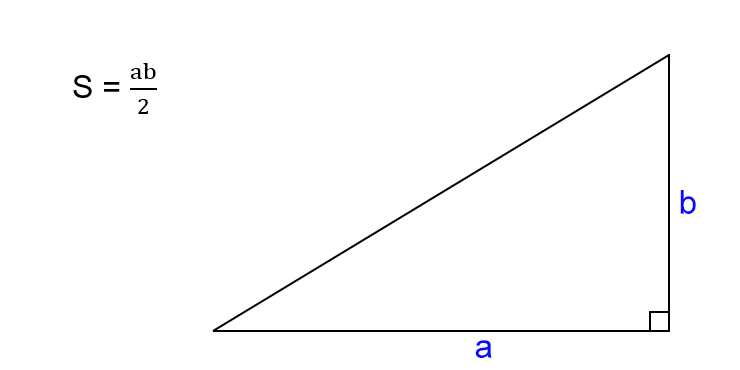
- S — искомая площадь треугольника.
- a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.
Как найти площадь равнобедренного треугольника
- Умножьте основание на высоту треугольника.
- Поделите результат на два.
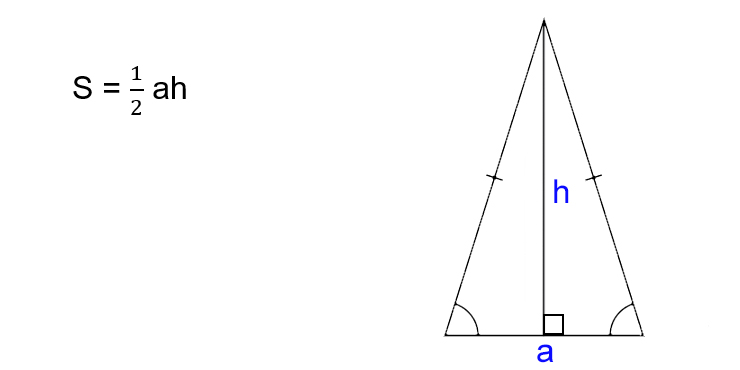
- S — искомая площадь треугольника.
- a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
- h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.
Как найти площадь равностороннего треугольника
- Умножьте квадрат стороны треугольника на корень из трёх.
- Поделите результат на четыре.
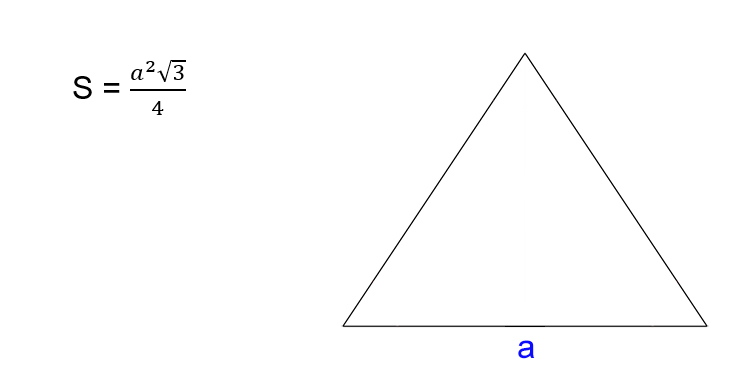
- S — искомая площадь треугольника.
- a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.
Читайте также 🧠👨🏻🎓✍🏻
Площадь треугольника
Таблица с формулами площади треугольника (в конце страницы)
Скачать формулы площади треугольника в виде картинки или файла PDF (в конце страницы)
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
Для всех треугольников
1
Площадь треугольника по основанию и высоте
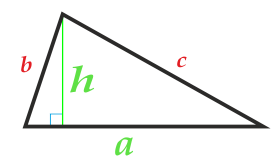
Сторона a
Высота h
Основанием треугольника может быть выбрана любая из сторон треугольника.
2
Площадь треугольника по двум сторонам и углу между ними
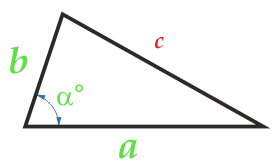
Сторона a
Сторона b
Угол α° между сторонами a и b
Угол α между сторонами может быть любым: тупым, острым, прямым.
3
Площадь треугольника по радиусу вписанной окружности и трем сторонам
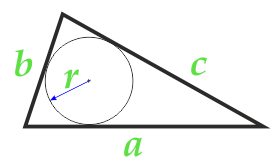
Сторона a
Сторона b
Сторона c
Радиус r вписанной окружности
4
Площадь треугольника по радиусу описанной окружности и трем сторонам
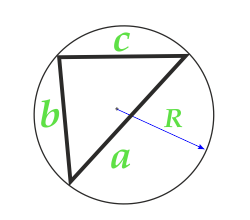
Сторона a
Сторона b
Сторона c
Радиус R описанной окружности
5
Площадь треугольника по формуле Герона
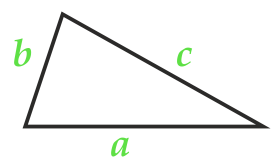
Полупериметр:
Сторона a
Сторона b
Сторона c
6
Площадь произвольного треугольника по стороне и двум прилежащим углам
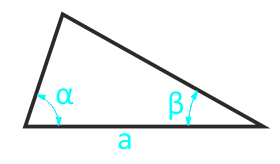
Сторона a
Угол β°
Угол α°
Для равнобедренных треугольников
7
Площадь равнобедренного треугольника по боковым сторонам и основанию
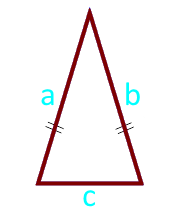
Сторона a (a = b)
Сторона c
8
Площадь равнобедренного треугольника по боковым сторонам и углу между ними
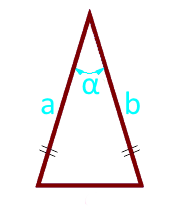
Боковая сторона a (a = b)
Угол α° между боковыми сторонами
9
Площадь равнобедренного треугольника по боковой стороне, основанию и углу между ними
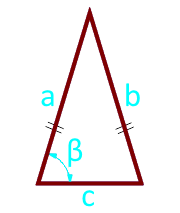
Боковая сторона a (a = b)
Основание треугольника c
Угол β° между основанием и стороной
10
Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами
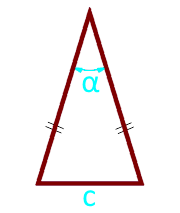
Основание треугольника c
Угол α° между боковыми сторонами
Для равносторонних треугольников
11
Площадь равнобедренного треугольника по высоте и основанию
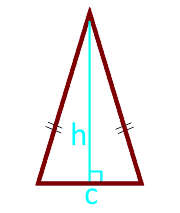
Основание треугольника c
Высота h
12
Площадь равностороннего треугольника по стороне
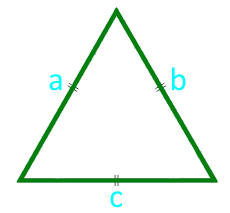
Сторона a (a = b = c)
13
Площадь равностороннего треугольника по высоте
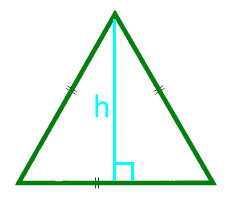
Высота h
14
Площадь равностороннего треугольника по радиусу вписанной окружности
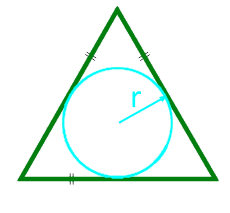
Радиус r вписанной окружности
15
Площадь равностороннего треугольника по радиусу описанной окружности
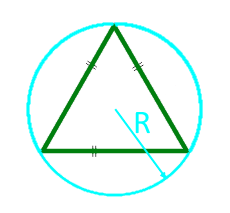
Радиус R описанной окружности
Для прямоугольных треугольников
16
Площадь прямоугольного треугольника по двум катетам
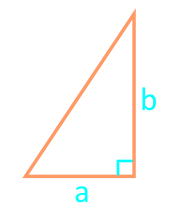
Катет a
Катет b
17
Площадь прямоугольного треугольника через гипотенузу и угол
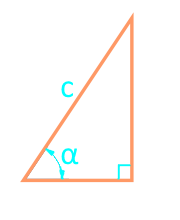
Сторона c
Угол α
18
Площадь прямоугольного треугольника через катет и угол
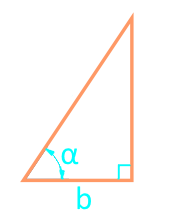
Сторона b
Угол α
19
Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность
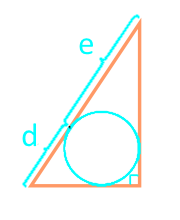
Отрезок d
Отрезок e
20
Площадь прямоугольного треугольника через гипотенузу и вписанную окружность
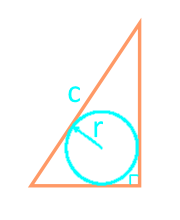
Сторона с
Радиус r
21
Площадь прямоугольного треугольника по формуле Герона
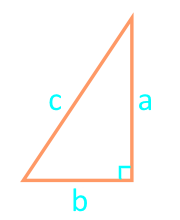
Полупериметр:
Сторона a
Сторона b
Сторона c
Для вычисления площади треугольника применяются различные формулы, в зависимости от известных исходных данных. Выше приведены формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные вычисления. Приведены общие формулы для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.
Наш калькулятор для вычисления площади поможет вам вычислить площадь разных видов треугольников или проверить уже выполненные вычисления.
В зависимости от вида треугольника и его известных исходных данных, площадь треугольника можно вычислить по различным формулам.
Таблица с формулами площади треугольника
Определения
Площадь треугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя отрезками (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой.
Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Скачать формулы площади треугольника в виде картинки
Площадь любого треугольника можно найти, зная основание и высоту. Вся простота схемы заключается в том, что высота делит основание a на две части a1 и a2, а сам треугольник – на два прямоугольных треугольника, площадь которых получается  и
и  . Тогда площадь всего треугольника будет суммой двух указанных площадей, и если мы вынесем одну вторую высоты за скобку, то в сумме мы получим обратно основание:
. Тогда площадь всего треугольника будет суммой двух указанных площадей, и если мы вынесем одну вторую высоты за скобку, то в сумме мы получим обратно основание: 
Более сложный для расчетов способ – это формула Герона, для которой необходимо знать все три стороны. Для этой формулы нужно вычислить сначала полупериметр треугольника:  Сама формула Герона подразумевает квадратный корень из полупериметра, умноженного поочередно на разность его с каждой из сторон.
Сама формула Герона подразумевает квадратный корень из полупериметра, умноженного поочередно на разность его с каждой из сторон.
Следующий способ, также актуальный для любого треугольника, позволяет найти площадь треугольника через две стороны и угол между ними. Доказательство этому проистекает из формулы с высотой – проводим высоту на любую из известных сторон и через синус угла α получаем, что h=a⋅sinα . Для вычисления площади умножим половину высоты на вторую сторону.
Другой способ – найти площадь треугольника, зная 2 угла и сторону между ними. Доказательство этой формулы достаточно простое, и наглядно видно из схемы.

Опускаем из вершины третьего угла высоту на известную сторону и называем полученные отрезки x соответственно. Из прямоугольных треугольников видно, что первый отрезок x равен произведению котангенса угла α на высоту, а второй отрезок y – произведению котангенса угла β на эту же высоту. Дальше соединяем это вместе:



Формулы площади треугольника
Формулы площади треугольника
Подождите пару секунд пока подгрузятся формулы
Внимание! Десятичную дробь надо писать с точкой(.), а не с запятой!
Через основание и высоту
 $$S= \frac{1}{2} ah $$
\(S\) — площадь треугольника
$$S= \frac{1}{2} ah $$
\(S\) — площадь треугольника\(a\) — основание
\(h\) — высота
\(a =\) \(h =\)
Через две стороны и угол
 $$S= \frac{1}{2} ab sin \alpha $$
\(S\) — площадь треугольника
$$S= \frac{1}{2} ab sin \alpha $$
\(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\( \alpha \) — угол между сторонами \(a\) и \(b\)
\(a =\) \(b =\) \( \alpha =\)
Формула Герона
 $$S= \sqrt{p(p-a)(p-b)(p-c)} $$
\(S\) — площадь треугольника
$$S= \sqrt{p(p-a)(p-b)(p-c)} $$
\(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\(c\) — сторона
\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
\(a =\) \(b =\) \(c =\)
Через радиус вписанной окружности
 $$S= rp $$
\(S\) — площадь треугольника
$$S= rp $$
\(S\) — площадь треугольника\(r\) — радиус вписанной окружности
\(a\) — сторона
\(b\) — сторона
\(c\) — сторона
\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
\(r =\) \(p =\)
Через радиус описанной окружности
 \(S= \frac{abc}{4R} \)
\(S= \frac{abc}{4R} \)\(S\) — площадь треугольника
\(R\) — радиус описанной окружности
\(a\) — сторона
\(b\) — сторона
\(c\) — сторона
\(a =\) \(b =\)
\(c =\) \(R =\)
Площадь прямоугольного треугольника
 $$S= \frac{1}{2} ab $$
\(S\) — площадь треугольника
$$S= \frac{1}{2} ab $$
\(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\(a =\) \(b =\)
Площадь прямоугольного треугольника
 $$S= de $$
\(S\) — площадь треугольника
$$S= de $$
\(S\) — площадь треугольника\(d =\) \(e =\)
Формула Герона для прямоугольного треугольника
 $$ S= (p-a)(p-b) $$
\(S\) — площадь треугольника
$$ S= (p-a)(p-b) $$
\(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
\(a =\) \(b =\) \(p =\)
Площадь равнобедренного треугольника
 $$S= \frac{1}{2} a^2 sin \alpha$$
\(S\) — площадь треугольника
$$S= \frac{1}{2} a^2 sin \alpha$$
\(S\) — площадь треугольника\(a\) — сторона
\(\alpha\) — угол между боковыми сторонами
\(a =\) \( \alpha =\)
Площадь равнобедренного треугольника

\(a\) — сторона
\(b\) — сторона
\(\alpha\) — угол между боковыми сторонами и основанием
\(a =\) \(b =\) \( \alpha =\)
Площадь равнобедренного треугольника
 $$S= \frac{b^2}{4tg \frac{ \alpha }{2}} $$
\(S\) — площадь треугольника
$$S= \frac{b^2}{4tg \frac{ \alpha }{2}} $$
\(S\) — площадь треугольника\(b\) — сторона
\(\alpha\) — угол между боковыми сторонами и основанием
\(b =\) \(\alpha =\)
Формула Герона для равнобедренного треугольника
a = b =Площадь равностороннего треугольника
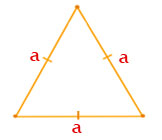 $$S= \frac{ \sqrt{3}a^2}{4} $$
\(S\) — площадь треугольника
$$S= \frac{ \sqrt{3}a^2}{4} $$
\(S\) — площадь треугольника\(a\) — сторона
\(a =\)
Площадь равностороннего треугольника
 $$S= \frac{3 \sqrt{3}R^2}{4}$$
\(S\) — площадь треугольника
$$S= \frac{3 \sqrt{3}R^2}{4}$$
\(S\) — площадь треугольника\(R\) — радиус описанной окружности
\(R =\)
Площадь равностороннего треугольника
 $$S= 3 \sqrt{3}r^2 $$
\(S\) — площадь треугольника
$$S= 3 \sqrt{3}r^2 $$
\(S\) — площадь треугольника\(r\) — радиус вписанной окружности
\(r =\)
Площадь равностороннего треугольника
 $$S= \frac{h^2}{\sqrt{3}}$$
\(S\) — площадь треугольника
$$S= \frac{h^2}{\sqrt{3}}$$
\(S\) — площадь треугольника\(h\) — высота
\(h =\)
Часто собственнику квартиры или дома требуется узнать площадь комнаты для ремонта или других целей. А как рассчитать её — не каждый знает, тем более, если помещение неправильной формы, а человек не силен в математике. Все не так трудно, как кажется. Достаточно разделить комнату на фигуры правильной формы, затем найти значения их площади и полученные величины сложить. Давайте рассмотрим данный вопрос вплотную.
Площадь считают по стенкам для покупки обоев, плитки, либо по полу, чтобы узнать квадратуру квартиры при покупке, продаже и т.п. Для точного измерения размеров стен, пола желательно освободить помещение от мебели. Если объект имеет форму квадрата или прямоугольника, то рассчитать площадь не составит особого труда. Вам потребуется взять лист бумаги, чтобы просчитать площади четырех стен, пола. Площадь прямоугольника равняется S = ab, т.е. произведению длины на высоту. Чтобы подсчитать площади всех стен, придется измерять их длину и высоту. Если же комната идеально ровная и вам не требуются точные подсчеты, то достаточно измерить длину и высоту двух прилежащих друг к другу стенок. Затем по этим данным посчитайте площадь меньшей стены (S1), большей (S2). А потом найдите S комнаты по формуле:Для расчета S комнаты по полу померьте ширину и длину пола, перемножьте значения.
- Sтреугольника = ½ ab, где a — основание треугольника, b — высота, проведенная к этому основанию.
- Sкруга = πR², где π = 3,14; R — радиус круга. Радиус легче измерить лазерной рулеткой . Показания, сделанные таким дальномером, будут точней.
- Sполукруга = ½ πR².
В конце просуммируйте все полученные результаты.
- Площадь пола;
- Площадь всех стен объекта.
После поданной информации вы с легкостью сможете узнать площадь вашей комнаты самостоятельно. И никаких
Формулы площадей всех основных фигур
1. Формула площади равнобедренной трапеции через стороны и угол

b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):



2. Формула площади равнобокой трапеции через радиус вписанной окружности

R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m — средняя линия трапеции
c — боковая сторона
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):

Треугольник Калькулятор
Пожалуйста, предоставьте 3 значения, включая как минимум одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать». Когда радианы выбраны в качестве единицы измерения угла, они могут принимать значения, такие как pi / 2, pi / 4 и т. Д.
Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, где встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединяются тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами.Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются исходя из длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют одинаковую длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют одинаковую длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковую длину, это называется разносторонним, как показано ниже.

Отметки на краю треугольника представляют собой обычное обозначение, которое отражает длину стороны, где одинаковое количество отметок означает равную длину.Аналогичные обозначения существуют для внутренних углов треугольника, обозначаемых различными числами концентрических дуг, расположенных в вершинах треугольника. Как видно из приведенных выше треугольников, длина и внутренние углы треугольника напрямую связаны, поэтому имеет смысл, что равносторонний треугольник имеет три равных внутренних угла и три стороны равной длины. Обратите внимание, что треугольник, представленный в калькуляторе, не показан в масштабе; хотя он выглядит равносторонним (и имеет угловые метки, которые обычно читаются как равные), он не обязательно является равносторонним и представляет собой просто представление треугольника.Когда вводятся фактические значения, вывод калькулятора будет отражать, как должна выглядеть форма входного треугольника.
Треугольники, классифицированные по их внутренним углам, делятся на две категории: прямые или наклонные. Прямой треугольник — это треугольник, в котором один из углов равен 90 °, и обозначается двумя отрезками, образующими квадрат в вершине, составляющей прямой угол. Самый длинный край прямоугольного треугольника, то есть край, противоположный прямому углу, называется гипотенузой.Любой треугольник, который не является прямоугольным, классифицируется как наклонный треугольник и может быть тупым или острым. В тупом треугольнике один из углов треугольника больше 90 °, а в остром треугольнике все углы меньше 90 °, как показано ниже.

Факты о треугольнике, теоремы и законы

- Учитывая длины всех трех сторон любого треугольника, каждый угол может быть рассчитан с использованием следующего уравнения.Обратитесь к треугольнику выше, предполагая, что a, b и c являются известными значениями.
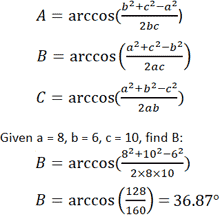
Площадь Треугольника
Существует несколько различных уравнений для расчета площади треугольника, в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для расчета площади треугольника включает его основание b и высоту h . «Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка, проведенного от вершины, противоположной основанию, до точки на основании, которая образует перпендикуляр.
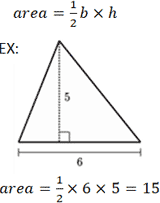
Учитывая длину двух сторон и угол между ними, следующая формула может быть использована для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному в калькуляторе выше. Дано a = 9, b = 7 и C = 30 °:
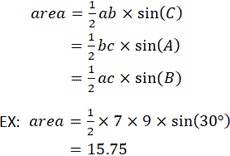
Другой метод расчета площади треугольника использует формулу Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат.Однако для этого требуется, чтобы длины трех сторон были известны. Опять же, со ссылкой на треугольник, представленный в калькуляторе, если a = 3, b = 4 и c = 5:
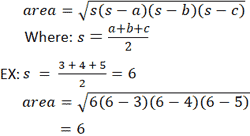
Медиана, инрадиус и оксирадиус
Медиана
Медиана треугольника определяется как длина отрезка, который простирается от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, все из которых будут пересекаться в центроиде (среднее арифметическое положение всех точек в треугольнике) треугольника.Обратитесь к рисунку, приведенному ниже, для пояснения.
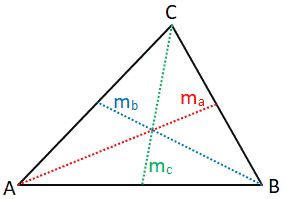
Медианы треугольника представлены отрезками линии m a , m b и m c . Длина каждой медианы может быть рассчитана следующим образом:
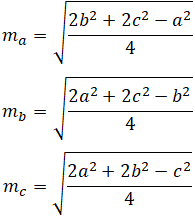
Где a, b и c представляют длину стороны треугольника, как показано на рисунке выше.
В качестве примера, учитывая, что a = 2, b = 3 и c = 4, медиана m и может быть рассчитана следующим образом:
Inradius
Инрадиус — это радиус самого большого круга, который будет помещаться внутри данного многоугольника, в данном случае, треугольника.Inradius перпендикулярен каждой стороне многоугольника. В треугольнике значение радиуса можно определить, построив две угловые биссектрисы для определения стимулятора треугольника. Inradius — это перпендикулярное расстояние между стимулятором и одной из сторон треугольника. Любая сторона треугольника может использоваться до тех пор, пока определяется перпендикулярное расстояние между стороной и стимулятором, так как стимулятор, по определению, равноудален от каждой стороны треугольника.
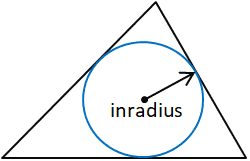
Для целей данного калькулятора, вычисление радиуса вычисляется с использованием площади (площади) и полупериметра (ов) треугольника, а также следующих формул:
, где a, b и c — стороны треугольника
Circumradius
Циррадиус определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника.Центр этого круга, где встречаются все перпендикулярные биссектрисы каждой стороны треугольника, является окружным центром треугольника и является точкой, из которой измеряется окружность. Окружный центр треугольника не обязательно должен быть внутри треугольника. Стоит отметить, что все треугольники имеют окружность (круг, проходящий через каждую вершину) и, следовательно, окружность.

Для целей данного калькулятора круговой луч рассчитывается по следующей формуле:
Где a — сторона треугольника, а A — угол, противоположный стороне a
Хотя используются сторона А и угол А, в формуле можно использовать любую из сторон и их соответствующие противоположные углы.
,Самый распространенный метод
Обычно называемая «половина высоты основания», площадь треугольника определяется по формуле ниже., где б длина базаа — длина соответствующего высота над уровнем моря
Вы можете выбрать любую сторону, чтобы быть основание. Это не обязательно должно быть то, что нарисовано внизу треугольника. Высота должен быть тем, который соответствует выбранной вами базе. Высота — это линия, перпендикулярная выбранному основанию от противоположной вершины.
На рисунке выше, одна сторона была выбрана в качестве базы, и показана соответствующая высота над уровнем моря.
Калькулятор
Используйте калькулятор выше, чтобы рассчитать площадь треугольника
Введите любые два значения, и другое будет рассчитано.Например: введите базу и высоту и нажмите «Рассчитать». Площадь будет рассчитана.
Точно так же, если вы введете площадь и базу, будет вычислена высота, необходимая для получения этой области.
Методы нахождения площади треугольника
Что попробовать
На рисунке выше, нажмите «стоп-высота». Теперь, когда вы перетаскиваете точку A, обратите внимание, что область не меняется. Площадь зависит от основания и высоты, и ни одна из них не изменяется при перемещении верхней вершины из стороны в сторону.Следовательно, все треугольники, которые вы можете создать таким образом, имеют одинаковую площадь.
Другие темы треугольника
Общие
Периметр / Площадь
Типы треугольников
Треугольные центры
Конгруэнтность и Сходство
Решение треугольников
Тесты по треугольнику и упражнения
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
Площадь Треугольников
Есть несколько способов найти площадь треугольника.
Знание базы и высоты
Когда мы знаем основание и высоту, это легко.
Это просто половина b раз ч
Площадь = 1 2 чч
(страница «Треугольники» объясняет больше)
Самое главное, чтобы основание и высота были под прямым углом.Поиграйте здесь:
Пример: какова площадь этого треугольника?
(примечание: 12 — высота , , а не длина левой стороны)
Высота = h = 12
Base = b = 20
Площадь = ½ чч = ½ × 20 × 12 = 120
Знание трех сторон
Существует также формула для определения площади любого треугольника, когда мы знаем длины всех трех его сторон.
Это можно найти на странице формулы Герона.
Знание двух сторон и включенного угла
Когда мы знаем две стороны и включенный угол (SAS), есть другая формула (фактически три эквивалентные формулы), которую мы можем использовать.
В зависимости от того, какие стороны и углы нам известны, формулу можно записать тремя способами:
Площадь = 1 2 ab sin C
Площадь = 1 2 до н.э. sin
Площадь = 1 2 ca sin B
Это действительно одна и та же формула, только с измененными сторонами и углом.
Пример: Найти площадь этого треугольника:
Прежде всего мы должны решить, что мы знаем.
Мы знаем угол C = 25º, а стороны a = 7 и b = 10.
Итак, начнем:
Площадь = (½) ab sin C
Введите значения, которые мы знаем: ½ × 7 × 10 × sin (25º)
Выполнить работу калькулятора: 35 × 0,4226 …
Площадь = 14,8 с точностью до одного знака после запятой
Как запомнить
Просто подумайте «abc»: Площадь = ½ a b sin C
Также хорошо помнить, что угол всегда составляет между двумя известными сторонами , называемыми «включенным углом».
Как это работает?
Мы знаем, как найти область, когда мы знаем основание и высоту:
Площадь = ½ × основание × высота
В этом треугольнике:
|
Итак, мы получаем:
Площадь = ½ × (с) × (b × грех A)
Что (проще):
Площадь = 1 2 до н.э. sin
Изменяя метки на треугольнике, мы также можем получить:
- Площадь = ½ ab sin C
- Площадь = ½ ca sin B
Еще один пример:
Пример: Найти, сколько земли
Фермер Джонс владеет треугольным участком земли.
Длина забора АВ составляет 150 м. Длина забора до н.э. составляет 231 м.
Угол между ограждением AB и ограждением BC составляет 123º.
Сколько земли принадлежит фермеру Джонсу?
Прежде всего мы должны решить, какие длины и углы мы знаем:
- AB = c = 150 м,
- г. до н.э. = а = 231 м,
- и угол B = 123º
Итак, мы используем:
Площадь = 1 2 ca sin B
Введите значения, которые мы знаем: ½ × 150 × 231 × грех (123º) м 2
Выполнить работу калькулятора: 17,325 × 0.838 … м 2
Площадь = 14 530 м 2
Фермер Джонс имеет 14 530 м 2 земли
,Как найти стороны прямоугольного треугольника
Существует несколько способов получения длины сторон прямоугольного треугольника. В зависимости от того, что дано, вы можете использовать различные отношения или законы, чтобы найти недостающую сторону:
- Учитывая две стороны
Если вы знаете две другие стороны прямоугольного треугольника, это самый простой вариант; все, что вам нужно сделать, это применить теорему Пифагора:
a² + b² = c²
, если нога
и— недостающая сторона, то преобразуйте уравнение в форму, когда a находится на одной стороне, и возьмите квадратный корень:a = √ (c² - b²), если нога
bнеизвестна, тоb = √ (c² - a²)для гипотенузы с отсутствует, формула
c = √ (a² + b²)
- Заданный угол и гипотенуза
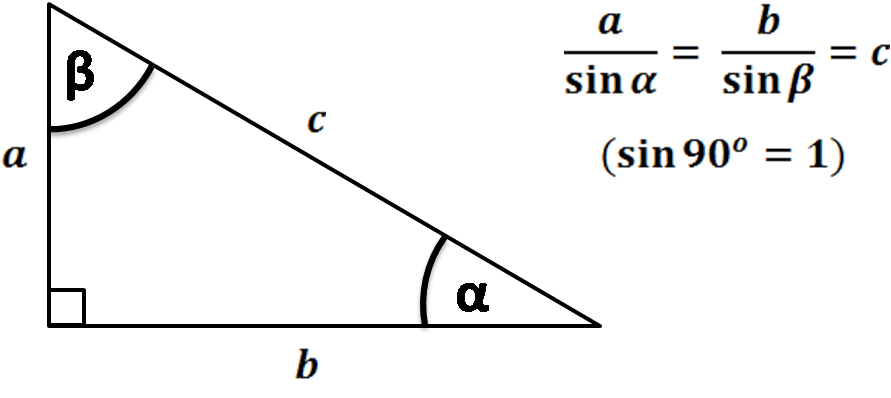
Примените закон синусов или тригонометрии, чтобы найти длины сторон правильного треугольника:
- Заданный угол и одна нога
Найдите недостающую ногу с помощью тригонометрических функций:
a = b * tan (α)b = a * tan (β)
- Заданная площадь и одна нога
Как мы помним из основной формулы площади треугольника, мы можем вычислить площадь, умножив высоту треугольника и основание и разделив результат на два.Прямой треугольник — это особый случай разностороннего треугольника, в котором одна ветвь является высотой, когда вторая ветвь является основанием, поэтому уравнение упрощается до:
площадь = a * b / 2
Например, если мы знаем только площадь прямоугольного треугольника и длину ноги и , мы можем вывести уравнение для других сторон:
-
b = 2 * площадь / -
c = √ (a² + (2 * площадь / a) ²)
