Развертка усеченного и прямого конуса
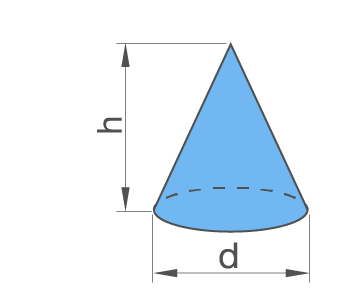
Расчёт развёртки конуса
Введите размеры в мм, и тип конуса:
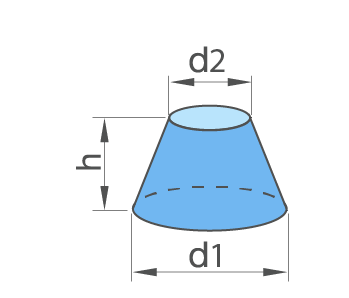
Результат расчёта:
Скачать, сохранить результат
Выберите способ сохранения
Информация
Часто в строительной практике или даже повседневной жизни приходится сталкиваться с необходимостью построения конуса. Процесс построения требует определенных знаний и высокой точности, иначе конус будет иметь определенные отклонения от необходимых параметров и это может привести к тем или иным неприятным последствиям. Расчет развертки конуса является важнейшей частью при создании выкройки для конуса. Данный показатель относительный и при его расчете необходимо знать ряд других параметров. При этом, необходимо понимать, что существует два вида конусов. Первый вид называется «Прямой конус», то есть классическом его понимании. Второй вид называется «Усеченный конус» — часть конуса, которая заключается между основанием и секущей плоскостью, параллельной его основанию. Расчет развертки прямого конуса отличается от того, как производится расчет развертки усеченного конуса. Отличие заключается в том, что у усеченного конуса появляется еще одна переменная и по итогу расчета калькулятор сообщает в расчете не только расстояние и угол, но и два радиуса.
Наш онлайн калькулятор имеет встроенные формулы, что позволяет производить расчет данных показателей, просто выбрав вид конуса и введя абсолютные значения в соответствующие ячейки. Возможности и принцип построения системы калькулятора исключают допущение ошибок при расчетах, и избавляют пользователя от необходимости в самостоятельном детальном изучении методик расчета.
Преимущества, которые дает онлайн калькулятор
- Большая экономия времени;
- Гарантированно правильный и предельно точный расчет;
- Удобный интерфейс, который будет понятен даже новичку;
- Открытый доступ к калькулятору для всех пользователей.
Таким образом, можно сделать вывод, что расчет развертки конуса требует концентрации внимания на многих деталях, и самостоятельный его расчет является достаточно трудоемким. Наш онлайн калькулятор является инструментом, который упростит Вашу жизнь при точном расчете данного показателя. Также Вам доступна информация о том, какая формула применяется при расчете и определенная справочная информация.
поделиться и оценить
Смотрите также:
Добавить комментарий
Онлайн калькулятор: Развертка (выкройка) сферы
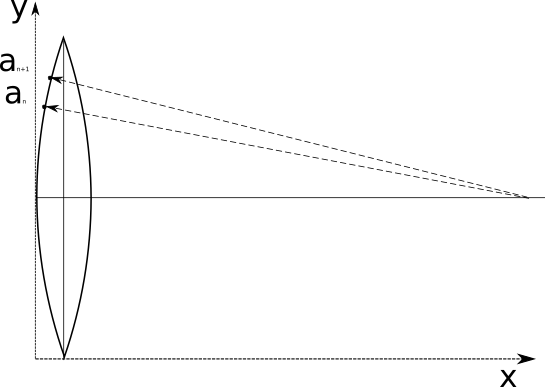
Калькулятор рассчитывает параметры развертки сферы на плоскости. Картинка ниже иллюстрирует задачу.
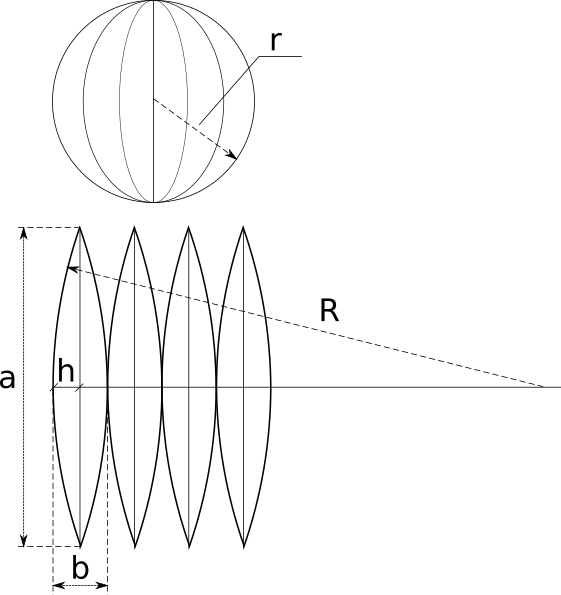
Итак, нам известен радиус сферы r и число долей на которое мы хотим ее разбить n. Для описания развертки нам надо найти высоту «дольки» a, ширину «дольки» b, и радиус R большой дуги, на которой построена «долька». Формулы расчета и объяснения, как обычно, приведены под калькулятором.

Развертка сферы
Сгенерировать точки разверткиТочность вычисленияЗнаков после запятой: 2
Высота доли (а)
Ширина доли (b)
Высота сегмента (h)
Радиус дуги (R)
save Сохранить extension Виджет
С высотой все понятно — это половина длины окружности, которую можно получить при сечении сферы плоскостью, проходящей через центр. Таким образом,
.
С шириной тоже все понятно — это часть той же окружности, полученная при разбиении всей окружности на n частей:
Радиус дуги можно вычислить по длине хорды (это
В принципе, найдя a и b, считать радиус R даже не обязательно — его можно найти по построению, что иллюстрирует следующая картинка.
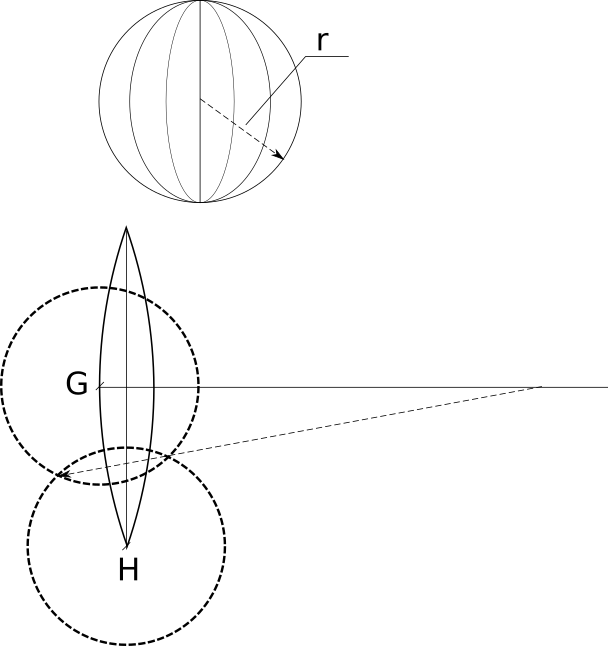
Для нахождения радиуса из точек G и H надо провести две окружности, так, чтобы они пересекались — прямая, проведенная через точки пересечения, пересечет среднюю линию в точке центра окружности, на дуге которой лежат G и H.
Несмотря на всю простоту, у метода есть один недостаток — а именно, ему нужно очень много места сбоку для радиуса, и чем больше число долек, на которое мы хотим разбить сферу, тем больше радиус большой дуги. Не везде будет возможность найти столько места и такой большой «циркуль», чтобы нарисовать дугу. Поэтому калькулятор, кроме расчета параметров «дольки», также рассчитывает координаты точек, лежащих на дуге — можно строить дуги дольки по точкам, не используя радиус. Для того, чтобы рассчитать координаты точек, надо пометить флажок «Сгенерировать точки развертки», и указать число точек — дуга будет разбита на заданное число точек с равным угловым шагом, как показано на рисунке:
Рассмотрим ситуацию, которая нередко возникает на гибочном производстве. Особенно это касается небольших цехов, которые обходятся средствами малой и средней механизации. Под малой и средней механизацией я подразумеваю использование ручных или полуавтоматических листогибов. Оператор суммирует длину полок, получает общую длину заготовки для требуемого изделия, отмеряет нужную длину, отрезает и.. после гибки получает неточное изделие. Погрешности размеров конечного изделия могут быть весьма значительными (зависит от сложности изделия, количества гибов и т.д.). Все потому, что при расчетах длины заготовки нужно учитывать толщину металла, радиус гибки, коэффициент положения нейтральной линии (К-фактор). Именно этому и будет посвящена данная статья.
Итак, приступим.
Честно говоря, произвести расчет размеров заготовки несложно. Нужно только понять, что нужно брать в расчет не только длины полок (прямых участков), но и длины криволинейных участков, получившихся ввиду пластических деформаций материала при гибке.
Притом, все формулы уже давно выведены «умными людьми», книги и ресурсы которых я постоянно указываю в конце статей (оттуда вы, при желании, можете получить дополнительные сведения).
Таким образом, для расчета правильной длины заготовки (развертки детали), обеспечивающей после гибки получение заданных размеров, необходимо, прежде всего, понять, по какому варианту мы будем производить расчет.
Напоминаю:
Таким образом, если вам нужна поверхность полки А без деформаций (например для расположения отверстий), то вы ведете расчет по варианту 1 . Если же вам важна общая высота полки А , тогда, без сомнения, вариант 2 более подходящий.
Вариант 1 (с припуском)
Нам понадобится:
в) Суммировать длины этих отрезков. При этом, длины прямых участков суммируются без изменения, а длины криволинейных участков – с учетом деформации материала и соответственного смещения нейтрального слоя.
Так, например, для заготовки с одним гибом, формула будет выглядеть следующим образом:
Где X 1 – длина первого прямого участка, Y 1 – длина второго прямого участка, φ – внешний угол, r – внутренний радиус гибки, k S – толщина металла.
Таким образом, ход расчета будет следующим..
Y1 + BA1 + X1 + BA2 + ..т.д
Длина формулы зависит от количества переменных.
Вариант 2 (с вычетом)
По моему опыту, это самый распространенный вариант расчетов для гибочных станков с поворотной балкой. Поэтому, давайте рассмотрим этот вариант.
Нам также необходимо:
а) Определить К-фактор (см таблицу).
б) Разбить контур изгибаемой детали на элементы, представляющие собой отрезки прямой и части окружностей;
Здесь необходимо рассмотреть новое понятие – внешняя граница гибки.
Чтобы было легче представить, см рисунок:
Внешняя граница гибки – вот эта воображаемая пунктирная линия.
Так вот, чтобы найти длину вычета, нужно от длины внешней границы отнять длину криволинейного участка.
Таким образом, формула длины заготовки по варианту 2:
Где Y 2 , X 2 – полки, φ – внешний угол, r – внутренний радиус гибки, k – коэффициент положения нейтральной линии (К-фактор), S – толщина металла.
Вычет у нас (BD ), как вы понимаете:
Внешняя граница гибки (OS ):
И в этом случае также необходимо каждую операцию рассчитывать последовательно. Ведь нам важна точная длина каждой полки.
Схема расчета следующая:
(Y2 – BD1 / 2) + (X2 – (BD1 / 2 + BD2 / 2)) + (M2 – (BD2 / 2 + BD3 /2)) + .. и т.д.
Графически это будет выглядеть так:
И еще, размер вычета (BD ) при последовательном расчете считать надо правильно. То есть, мы не просто сокращаем двойку. Сначала считаем весь BD , и только после этого получившийся результат делим пополам.
Надеюсь, что этой своей ремаркой я никого не обидел. Просто я знаю, что математика забывается и даже элементарные вычисления могут таить в себе никому не нужные сюрпризы.
На этом все. Всем спасибо за внимание.
При подготовке информации я использовал: 1. Статья «BendWorks. The fine-art of Sheet Metal Bending» Olaf Diegel, Complete Design Services, July 2002; 2. Романовский В.П. «Справочник по холодной штамповке» 1979г; материалы англоязычного ресурса SheetMetal.Me (раздел “Fabrication formulas”, ссылка:
§ 26. Общие сведения
Гибка — способ обработки металла давлением, при котором заготовке или ее части придается изогнутая форма. Слесарная гибка выполняется молотками (лучше с мягкими бойками) в
Рассчитать площадь поверхности или сечения трубопровода помогает формула длины развертки заготовки трубы. Расчет основывается на величине будущей трассы и диаметре планируемой конструкции. В каких случаях требуются такие вычисления и как они делаются, расскажет данная статья.
Когда нужны расчеты
Параметры рассчитываются на калькуляторе или с помощью онлайн-программ
Какую площадь должна иметь поверхность трубопровода, важно знать в следующих случаях.
- При расчете теплоотдачи «теплого» пола или регистра. Здесь высчитывается суммарная площадь, которая отдает помещению тепло, исходящее из теплоносителя.
- Когда определяются потери тепла по пути от источника тепловой энергии к обогревательным элементам – радиаторам, конвекторам и т.д. Чтобы определить количество и размеры таких приборов, нужно знать величину калорий, которой мы должны располагать, а она выводится с учетом развертки трубы.
- Для определения необходимого количества теплоизоляционного материала , антикоррозийного покрытия и краски. При строительстве магистралей протяженностью в километры, точный расчет экономит предприятию немалые средства.
- При определении рационально оправданного сечения профиля, которое могло бы обеспечить максимальную проводимость водопроводной или отопительной сети.
Определение параметров трубы
Площадь сечения
Труба представляет собой цилиндр, поэтому производить расчеты не сложно
Сечение круглого профиля – это круг, диаметр которого определяется, как разница величины наружного диаметра изделия за вычетом толщины стенок.
В геометрии площадь круга рассчитывается так:
S = π R^2 или S= π (D/2-N)^2, где S – площадь внутреннего сечения; π – число «пи»; R – радиус сечения; D — наружный диаметр; N — толщина стенок трубы.
Обратите внимание! Если в напорных системах жидкость заполняет весь объем трубопровода, то в самотечной канализации постоянно смачивается только часть стенок. В таких коллекторах применяется понятие площади живого сечения трубы.
Внешняя поверхность
Поверхность цилиндра, которым и является круглый профиль, представляет собой прямоугольник. Одна сторона фигуры – длина отрезка трубопровода, а вторая – величина окружности цилиндра.
Расчет развертки трубы осуществляется по формуле:
S = π D L, где S – площадь трубы, L – длина изделия.
Внутренняя поверхность
Такой показатель применяется в процессе гидродинамических расчетов, когда определяется площадь поверхности трубы, которая постоянно контактирует с водой.
При определении данного параметра следует учитывать:
- Чем больше диаметр водопроводных труб , тем меньше скорость проходящего потока зависит от шероховатости стенок конструкции.
На заметку! Если трубопроводы с большим диаметром характеризуются малой протяженностью, то величиной сопротивления стенок можно пренебречь.
- При гидродинамических расчетах шероховатости поверхности стенок придается не меньшее значение, чем ее площади. Если вода проходит по ржавому внутри водопроводу, то ее скорость меньше скорости жидкости, которая протекает по сравнительно гладкой полипропиленовой конструкции.
- Сети, которые монтируются из не оцинкованной стали, отличаются непостоянной площадью внутренней поверхности. При эксплуатации они покрываются ржавчиной и зарастают минеральными отложениями, из-за чего сужается просвет трубопровода.
Важно! Обратите внимание на этот факт, если захотите сделать холодное водоснабжение из стального материала. Проходимость такого водопровода сократится в два раза уже после десяти лет эксплуатации.
Расчет развертки трубы в данном случае делается с учетом того, что внутренний диаметр цилиндра определяется, как разность внешнего диаметра профиля и увеличенной вдвое толщины его стенок.
В результате площадь поверхности цилиндра определяется по формуле:
S= π (D-2N)L, где к уже известным параметрам добавляется показатель N, определяющий толщину стенок.

Формула развертки заготовки помогает рассчитать количество необходимой теплоизоляции
Чтобы знать, как посчитать развертку трубы, достаточно вспомнить курс геометрии, которую осваивают в средних классах. Приятно, что школьная программа находит применение во взрослой жизни и помогает решать серьезные задачи, связанные со строительством. Пусть они окажутся полезными и для вас!
§ 26. Общие сведения
Гибка — способ обработки металла давлением, при котором заготовке или ее части придается изогнутая форма. Слесарная гибка выполняется молотками (лучше с мягкими бойками) в тисках, на плите или с помощью специальных приспособлений. Тонкий листовой металл гнут киянками, изделия из проволоки диаметром до 3 мм — плоскогубцами или круглогубцами. Гибке подвергают только пластичный материал.
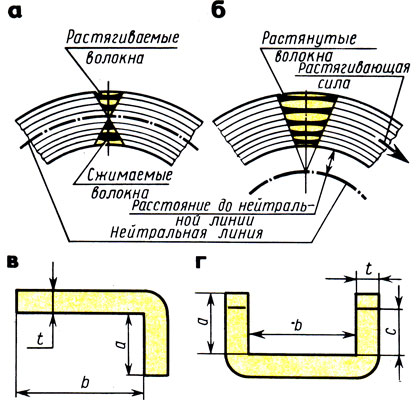
Гибка деталей — одна из наиболее распространенных слесарных операций. Изготовление деталей гибкой возможно как вручную на опорном инструменте и оправках, так и на гибочных машинах (прессах).
Сущность гибки заключается в том, что одна часть заготовки перегибается по отношению к другой на заданный угол. Происходит это следующим образом: на заготовку, свободно лежащую на двух опорах, действует изгибающая сила, которая вызывает в загото
Калькуляторы расчета размеров развертки конуса
Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.
 Калькуляторы расчета размеров развертки конуса
Калькуляторы расчета размеров развертки конусаЧтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.
Калькуляторы расчета размеров развертки конуса
Несколько слов о рассчитываемых параметрах
Понять принцип расчета будет несложно, разобравшись со следующей схемой:
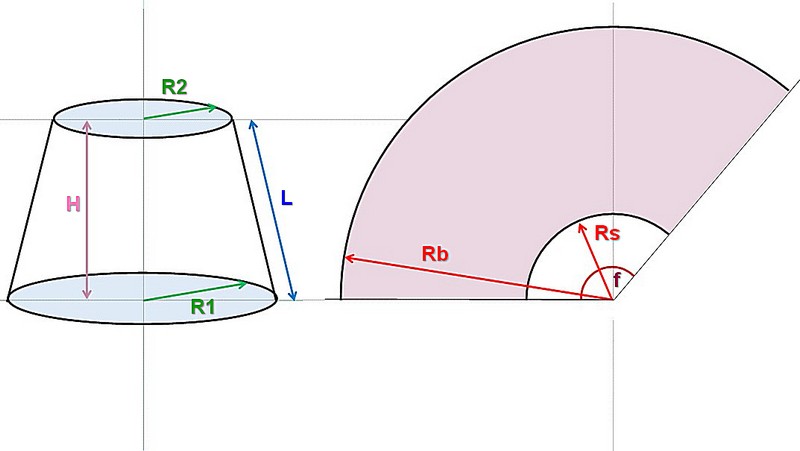 Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.
Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.
Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.
Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L
Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.
Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:
Шаг 1 – определение длины образующей L
(Если она уже известна – шаг пропускается)
Перейти к расчётам
Шаг 2 – определение радиусов внутренней и внешней дуги развертки
Радиусы рассчитываются поочередно – с выбором в соответствующем поле калькулятора.
Шаг 3 – определение величины центрального угла f
Перейти к расчётам
* * * * * * *
Итак, все данные имеются. Остается на листе бумаги циркулем провести две дуги рассчитанных радиусов. А затем из точки центра с помощью транспортира прочертить два луча под рассчитанным углом – они ограничат развертку по угловой длине.
Существуют и чисто геометрические методы построения довольно точной развертки конуса, без проведения расчётов. Один из них подробно описан в статье нашего портала «Как сделать абажур своими руками».
Развертка конуса — онлайн калькулятор
Данный калькулятор может пригодится инженерам-технологам или инженерам-конструкторам, то есть всем тем, кому часто приходится рассчитывать развертку прямого конуса обычного и усеченного.
Сам калькулятор ниже, он может рассчитать все необходимые параметры развертки прямого кругового конуса.
Калькулятор рассчитывает параметры развертки прямого кругового конуса на плоскости — визуально это можно посмотреть на рисунке внизу.
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
Рассчитать площадь поверхности или сечения трубопровода помогает формула длины развертки заготовки трубы. Расчет основывается на величине будущей трассы и диаметре планируемой конструкции. В каких случаях требуются такие вычисления и как они делаются, расскажет данная статья.
Когда нужны расчеты
Параметры рассчитываются на калькуляторе или с помощью онлайн-программ
Какую площадь должна иметь поверхность трубопровода, важно знать в следующих случаях.
- При расчете теплоотдачи «теплого» пола или регистра. Здесь высчитывается суммарная площадь, которая отдает помещению тепло, исходящее из теплоносителя.
- Когда определяются потери тепла по пути от источника тепловой энергии к обогревательным элементам – радиаторам, конвекторам и т.д. Чтобы определить количество и размеры таких приборов, нужно знать величину калорий, которой мы должны располагать, а она выводится с учетом развертки трубы.
- Для определения необходимого количества теплоизоляционного материала, антикоррозийного покрытия и краски. При строительстве магистралей протяженностью в километры, точный расчет экономит предприятию немалые средства.
- При определении рационально оправданного сечения профиля, которое могло бы обеспечить максимальную проводимость водопроводной или отопительной сети.
Определение параметров трубы
Площадь сечения

Труба представляет собой цилиндр, поэтому производить расчеты не сложно
Сечение круглого профиля – это круг, диаметр которого определяется, как разница величины наружного диаметра изделия за вычетом толщины стенок.
В геометрии площадь круга рассчитывается так:
S = π R^2 или S= π (D/2-N)^2, где S – площадь внутреннего сечения; π – число «пи»; R – радиус сечения; D — наружный диаметр; N — толщина стенок трубы.
Обратите внимание! Если в напорных системах жидкость заполняет весь объем трубопровода, то в самотечной канализации постоянно смачивается только часть стенок. В таких коллекторах применяется понятие площади живого сечения трубы.
Внешняя поверхность
Поверхность цилиндра, которым и является круглый профиль, представляет собой прямоугольник. Одна сторона фигуры – длина отрезка трубопровода, а вторая – величина окружности цилиндра.
Расчет развертки трубы осуществляется по формуле:
S = π D L, где S – площадь трубы, L – длина изделия.
Внутренняя поверхность
Такой показатель применяется в процессе гидродинамических расчетов, когда определяется площадь поверхности трубы, которая постоянно контактирует с водой.
При определении данного параметра следует учитывать:
- Чем больше диаметр водопроводных труб, тем меньше скорость проходящего потока зависит от шероховатости стенок конструкции.
На заметку! Если труб
Высокоточный калькулятор
- Цель использования
- Решить проблему
- Комментарий / Запрос
- Дайте мне пример цикла, пожалуйста?
Для (a = 1; a = 32; a = a + 1) {print (a * pi)}Что не так, пожалуйста?
[1] 2020/07/23 00:46 Мужчина / 60 лет или старше / Учитель / Исследователь / Очень /
- Цель использования
- Видя, насколько велики будут мои взрывы во время создания мода.Очень полезно будет использовать снова. : D
[2] 2020/07/21 15:24 Мужчины / До 20 лет / Самозанятые / Очень /
- Цель использования
- Поисковые расчеты в поддержку исследований
[3] 2020/07/21 07:25 Мужчина / 60 лет или старше / Учитель / Исследователь / Очень /
- Цель использования
- Вычисления в поддержку исследований
- Комментарий / Запрос
- Очень полезный и по-видимому уникальный интернет-ресурс.
[4] 2020/07/18 05:36 Мужчина / 60 лет или старше / Пенсионер / Очень /
- Цель использования
- Баскетбольные расчеты
[5] 2020/07/03 15:05 Мужчина / 20 лет / Инженер / Очень /
- Цель использования
- Проверьте решения при решении математических тестов
[6] 2020/06/30 18:38 Мужчина / Младше 20 лет / Высшая школа / Университет / Аспирант / Очень /
- Цель использования
- Рассчитать
[7] 2020/06/10 11:16 Мужчина / 20 лет / Высшая школа / Университет / Аспирант / Очень /
- Цель использования
- — собирается в цикл — с запада на восток — из Лос-Анджелеса в Бостон — список ведра — (исследование «ежедневных» потребностей в питании)
цикл на всю жизнь
[8] 2020/05/30 08:30 Мужчина / 60 лет или старше / Инженер / Полезно /
- Цель использования
- Я только что увидел это, глядя на калькулятор метрических конверсий, и попробовал.
- Комментарий / Запрос
- Это здорово, но я прошу добавить секущий, косеканс и котангенс.
[9] 2020/05/29 09:27 мужчина / младше 20 лет / начальная школа / младший школьник / полезно /
- Цель использования
- Чтобы вычислить cos (cos (cos (….. x) к большему числу цифр.
[10] 2020/05/23 02:38 Мужчина / 20 лет / Инженер / Полезно /
Калькулятор смешанных чисел
Использование калькулятора
Выполните математические вычисления со смешанными числами (смешанными дробями), выполняя операции над дробями, целыми числами, целыми числами, смешанными числами, смешанными дробями и неправильными дробями. Калькулятор смешанных чисел может складывать, вычитать, умножать и делить смешанные числа и дроби.
Калькулятор смешанных чисел (также называемый смешанными дробями):
Этот онлайн-калькулятор обрабатывает простые операции над целыми числами, целыми, смешанными числами, дробями и неправильными дробями путем сложения, вычитания, деления или умножения.Ответ предоставляется в сокращенной дроби и смешанном числе, если он существует.
Введите смешанные числа, целые числа или дроби в следующих форматах:
- Смешанные числа: введите как 1 1/2, что составляет половину или 25 3/32, что составляет двадцать пять и три тридцать секунды. Оставьте ровно один пробел между целым числом и дробью и используйте косую черту для ввода дроби. Вы можете ввести до 3 цифр в длину для каждого целого числа, числителя или знаменателя (123 456/789).
- Всего номеров: до 3 цифр в длину.
- Доли: введите как 3/4, что составляет три четверти, или 3/100, что составляет три сотых. Вы можете ввести до 3 цифр для каждого числителя и знаменателя (например, 456/789).
Добавление смешанных чисел с использованием формулы добавления фракций
- Преобразовать смешанные числа в неправильные дроби
- Используйте алгебраическую формулу для сложения дробей:
a / b + c / d = (ad + bc) / bd - Сократить дроби и упростить, если возможно
Формула добавления фракций
\ (\ dfrac {a} {b} + \ dfrac {c} {d} = \ dfrac {(a \ times d) + (b \ times c)} {b \ times d} \)
Пример
Добавить 1 2/6 и 2 1/4
\ (1 \ dfrac {2} {6} + 2 \ dfrac {1} {4} = \ dfrac {8} {6} + \ dfrac {9} {4} \)
\ (= \ dfrac {(8 \ times 4) + (9 \ times 6)} {6 \ times 4} \)
\ (= \ dfrac {32 + 54} {24} = \ dfrac {86} {24} = \ dfrac {43} {12} \)
\ (= 3 \ dfrac {7} {12} \)
1 2/6 + 2 1/4 = 8/6 + 9/4 = (8 * 4 + 9 * 6) / 6 * 4 = 86/24
Итак, мы получаем 86/24 и упрощаем до 3 7/12
вычитание смешанных чисел с использованием формулы вычитания фракций
- Преобразовать смешанные числа в неправильные дроби
- Используйте алгебраическую формулу для вычитания дробей: a / b — c / d = (ad — bc) / bd
- Сократить дроби и упростить, если возможно
Формула вычитания фракций
\ (\ dfrac {a} {b} — \ dfrac {c} {d} = \ dfrac {(a \ times d) — (b \ times c)} {b \ times d} \)
Пример
Вычтите 2 1/4 из 1 2/6
1 2/6 — 2 1/4 = 8/6 — 9/4 = (8 * 4 — 9 * 6) / 6 * 4 = -22 / 24
Уменьшите дробь до -11/12
Умножение смешанных чисел с использованием формулы умножения дробей
- Преобразовать смешанные числа в неправильные дроби
- Используйте алгебраическую формулу для умножения дробей: a / b * c / d = ac / bd
- Сократить дроби и упростить, если возможно
Формула умножения дробей
\ (\ dfrac {a} {b} \ times \ dfrac {c} {d} = \ dfrac {a \ times c} {b \ times d} \)
Пример
умножить 1 2/6 на 2 1/4
1 2/6 * 2 1/4 = 8/6 * 9/4 = 8 * 9/6 * 4 = 72/24
Уменьшите дробь до 3/1 и упростите до 3
Разделение смешанных чисел по формуле
.- Преобразовать смешанные числа в неправильные дроби
- Используйте алгебраическую формулу для деления дробей: a / b ÷ c / d = ad / bc
- Сократить дроби и упростить, если возможно
Формула разделения фракций
\ (\ dfrac {a} {b} \ div \ dfrac {c} {d} = \ dfrac {a \ times d} {b \ times c} \)
Пример
разделить 1 2/6 на 2 1/4
1 2/6 ÷ 2 1/4 = 8/6 ÷ 9/4 = 8 * 4/9 * 6 = 32/54
Уменьшите дробь, чтобы получить 16/27
Похожие калькуляторы
Для выполнения математических операций над простыми правильными или неправильными дробями используйте наш Калькулятор фракций.Этот калькулятор упрощает неправильные дробные ответы в смешанные числа.
Если вы хотите упростить отдельную дробь до минимальных сроков, используйте наш Упростить калькулятор фракций.
Для объяснения того, как разложить числа, чтобы найти наибольший общий множитель (GCF), см. Величайший калькулятор общего фактора.
Если вы упрощаете большие дроби вручную, вы можете использовать Длинное деление с калькулятором остатков, чтобы найти целые числа и значения остатка.
Примечание:
Этот калькулятор выполняет расчет сокращения быстрее, чем другие, которые вы можете найти. Основная причина в том, что код использует теорему Евклида для сокращения дробей, которые можно найти в Математический форум: LCD, LCM.
,Калькулятор кругаКруглая форма
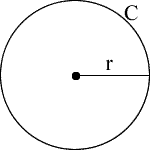
r = радиус
d = диаметр
C = окружность
A = площадь
π = pi = 3,1415926535898
√ = квадратный корень
Использование
Используйте этот калькулятор кругов, чтобы найти площадь, окружность, радиус или диаметр круга.Учитывая любую переменную A, C, r или d окружности, вы можете вычислить три других неизвестных.
Единицы: Обратите внимание, что единицы длины указаны для удобства. Они не влияют на расчеты. Единицы измерения установлены для указания порядка результатов, таких как футы, футы 2 или футы 3 . Любая другая базовая единица может быть заменена.
Формулы окружностей в терминах Pi π, радиуса r и диаметра d
радиус и диаметр:
р = д / 2
д = 2рПлощадь круга:
A = № 2 = № 2 /4
Окружность круга:
C = 2πr = πd
Круг Расчет:
С помощью приведенных выше формул и дополнительных формул вы можете вычислить свойства заданного круга для любой заданной переменной.2 \]
\ [C = 2 \ pi r \]
\ [d = 2r \]
Рассчитайте r, C и d | Учитывая A
По заданной площади круга рассчитать радиус, окружность и диаметр. Положив r, C и d в терминах A, получим следующие уравнения:
\ [r = \ sqrt {\ frac {A} {\ pi}} \]
\ [C = 2 \ pi r = 2 \ pi \ sqrt {\ frac {A} {\ pi}} \]
\ [d = 2r = 2 \ sqrt {\ frac {A} {\ pi}} \]
Рассчитайте A, r и d | Учитывая C
Учитывая окружность круга рассчитать радиус, площадь и диаметр.2} {4} \]
\ [C = 2 \ pi r = 2 \ pi \ frac {d} {2} = \ pi d \]
,Speed Distance Time Calculator
Использование калькулятора
Рассчитайте скорость, расстояние или время по формуле d = st, расстояние равно скорости и времени. Калькулятор времени и скорости можно найти для неизвестного. SDT значение с учетом двух известных значений.
Время может быть введено или определено в единицах секунд (секунд), минутах (минутах), часах (часах) или часах, минутах и секундах (чч: мм: сс).Видеть Ярлыки для форматов времени ниже.
Для определения расстояния используйте формулу для расстояния d = st, или расстояние равно скорости, умноженной на время.
расстояние = скорость х время
Скорость и скорость похожи, так как они представляют некоторое расстояние в единицу времени, например, мили в час или километры в час. Если ставка r соответствует скорости с , r = s = д / т.Вы можете использовать эквивалентную формулу d = rt, которая означает, что расстояние равно скорости, умноженной на время.
расстояние = скорость х время
Для определения скорости или скорости используйте формулу для скорости, s = d / t, что означает, что скорость равна расстоянию, деленному на время.
скорость = расстояние / время
Чтобы решить для времени, используйте формулу для времени, t = d / s, что означает, что время равно расстоянию, деленному на скорость.
время = расстояние / скорость
Форматы ввода времени чч: мм: сс
Вы можете использовать тире (-), точку (.) Или двоеточие (:) в качестве разделителей и всегда должны использовать 2 разделителя. Например, 15-06-22, 15.06.22 и 15:06:22 интерпретируются как 15 часов 6 минут 22 секунды или 15:06:22.
Допустимые пределы входа:
- часов от 0 до 999
- минут от 0 до 59
- секунд от 0 до 59
Ярлыки формата времени
X.,
5 ..
5 часов: 0 минут: 0 секунд
05:00:00
X.Y.
5,22.
5 часов: 22 минуты: 0 секунд
05:22:00
X.Y.Z
5.22,10
5.01.15
5.3.6
5 часов: 22 минуты: 10 секунд
5 часов: 1 минута: 15 секунд
5 часов: 3 минуты: 6 секунд
05:22:10
05:01:15
05:03:06
Y.
.22.
22 минуты
00:22:00
.Y.Z
.22,15
22 минуты: 15 секунд
00:22:15
..Z
.5
5 секунд
00:00:05
X..Z
5,05
5 часов: 0 минут: 5 секунд
05:00:05
Похожие калькуляторы
Для физических расчетов со скоростью, смещением и скоростью используйте наш Калькулятор смещения, чтобы решить для смещения с , средняя скорость v или время т .
,
 Существуют и чисто геометрические методы построения довольно точной развертки конуса, без проведения расчётов. Один из них подробно описан в статье нашего портала «Как сделать абажур своими руками».
Существуют и чисто геометрические методы построения довольно точной развертки конуса, без проведения расчётов. Один из них подробно описан в статье нашего портала «Как сделать абажур своими руками».