Проектирование дома по золотому сечению
Проектирование дома по золотому сечению


В течение многих столетий золотое сечение является основой архитектуры, живописи и других искусств. Золотое сечение — это природная гармония, пропорциональность, найти которую можно в самых разных живых структурах — в рисунке волокон дерева, в расположении лепестков цветов, в строении раковин и человеческого тела. Именно поэтому с самых древних времен человечество стремится использовать эту гармонию в повседневной жизни, в том числе и в строительстве.
Само понятие золотого сечения было введено греческим философом Пифагором, который сумел вывести формулу так называемой «божественной» пропорции. Он определил ее, как деление целого на две неравные части, при этом меньшая часть относится к большей точно так же, как большая к общему целому. Если за целое будет взята единица, то большая ее часть будет составлять 0,618, а меньшая — 0,382. Именно эти цифры можно использовать при
Как использовать золотое сечение в строительстве?


Все важные особенности будущего здания должны быть заложены в него еще на стадиях проектирования. Планирование строительства по золотому сечению начинается с определения главного модуля здания, который будет выступать условной единицей. Именно к нему впоследствии будут привязаны все остальные размеры объекта, и с его учетом будет разделяться внутреннее пространство объекта на секции.
В качестве модуля, важнейшей величины будущего строения можно взять средний человеческий рост или число, примерно соответствующее росту будущего собственника. Таким образом, владелец сможет спланировать строительство объекта, который будет максимально соответствовать ему самому.
Остальные выполняемые проектные и строительные работы будут зависеть от того, какую именно цель преследует собственник. Правило золотого сечения можно использовать не только при строительстве объектов, но также при проектировании отделки домов внутри и снаружи.
Где можно использовать золотое сечение?


Желая построить максимально функциональный и привлекательный жилой дом, собственник может использовать правило золотого сечения при определении соотношения цветов для оформления фасада или облицовки внутренних помещений. Учитывая это правило становится понятным, что для оформления комнаты или всего здания нужно будет использовать два цвета, причем, один из них будет доминирующим, занимающим около 60% всего оформляемого пространства, а второй — сопровождающим, занимающим от 30% до 40%. В интерьер можно также ввести и дополнительный цвет, которого должно быть не более 10%, его можно использовать для того, чтобы подчеркивать отдельные элементы декора или конструктивные детали здания.
Что касается самих цветов, то их выбирают с учетом стиля архитектуры и дизайна. Основной, сопровождающий и дополнительный цвета не обязательно должны сильно отличаться друг от друга. Иногда для оформления комнат можно использовать несколько оттенков одного цвета, делая мягкие переходы тональности и добиваясь, таким образом, нужного визуального эффекта.


Правило золотого сечения можно использовать и при создании общей дизайнерской композиции внешней или внутренней отделки. В этом случае выбирается главная деталь композиции, важнейшая фокусная точка освещения, меблировки и декора. Окружающее пространство заполняется аккомпанирующими элементами, которые подчеркивают выбранный стиль, главные конструктивные или дизайнерские решения. Опытные дизайнеры знают, что в любом интерьере должна быть динамика и развитие. Одноцветные и однородные дома не привлекают внимания, выглядят серо и совершенно не интересно.
Можно использовать золотое сечение и при делении стен на уровни. Для этого можно применять различные физические элементы, к примеру плинтуса. Если собственник хочет выполнить деление мягко и менее заметно, то стену можно оставить единым целым, применив принцип золотого сечения в расстановке мебели или в развеске панно. При таком способе оформления интерьера лучше использовать максимально нейтральный основной цвет, выставив на первый план яркие пятна декоративных элементов и всевозможных украшений.


Очень важно при оформлении здания выдержать правильное соотношение мебели и доступного пространства. С учетом правила золотого сечения, мебель в каждой комнате должна занимать не более 60% от общей композиции, иначе помещения будут выглядеть тесными и захламленными. До максимума повысить привлекательность и гармоничность внутренних помещений можно за счет проектирования мебели на заказ. В этом случае собственник сможет с учетом правила золотого сечения определить размеры и характеристики каждого отдельного элемента интерьера.
Правило 2/3 можно использовать практически при решении каждого вопроса, касающегося оформления комнат жилого дома. Так, при выборе подвесного светильника нужно учитывать, что он должен располагаться на высоте около 2/3 от высоты комнаты, диван должен занимать не больше 2/3 от выделенного под него простенка, журнальный столик должен быть больше 2/3 от размеров дивана, рядом с которым он располагается.
Правило золотого сечения можно использовать при проектировании придомовых территорий многоквартирных домов и частных строений, однако такие работы являются чрезвычайно сложными в выполнении, из-за чего к их реализации рекомендуется привлекать опытных проектировщиков. Для определения стоимости услуг специалистов можно воспользоваться калькулятором.
Поделитесь ссылкой
Дата публикации: 16.02.2017
как правильно рассчитать масштаб и пропорции дома Строительство по принципу золотого сечения
Ещё один инструмент в арсенале архитектора – это масштаб и пропорции. Они относится к тому, как отдельные части здания связаны друг с другом и с тем, как в целом необычный дом гармонирует с окружающим ландшафтом.
Обратите внимание, что масштаб необязательно означает размер. Апартаменты могут быть довольно большими, но иметь комфортную и интимную для человека обстановку. И наоборот. В маленьком домике можно жить вполне прекрасно с использованием маленьких элементов и других конструктивных особенностей.
Некоторые дизайнеры и архитекторы интуитивно проектируют строения с великолепными пропорциями, другие применяют такие системы, как золотое сечение. Сегодня мы вас познакомим с тем, как использовать эти инструменты при разработке собственного творческого шедевра.
1. Сформируйте уголки в большом доме
Этот особняк был разделён на отдельные области, каждая из который с собственной крышей, придающей ему визуально меньший облик. Материалы, палитра и пропорций связывают различные части вместе, а также резиденцию с окружающими холмами и зелёными насаждениями .

Проект от Mahoney Architects & Interiors
2. Создайте интересную композицию в ландшафте
Домик в поле или на другой обширной территории должен обладать эффектом присутствия. Для этого используйте смелые цвета или архитектурной детали, способный подчеркнуть его внешний облик.

Декор от Eck | MacNeely Architects inc.
3. Изменение масштаба по мере приближения к дому
Уменьшите размер архитектурных деталей, поскольку существует прямая зависимость между человеческим телом и габаритами сооружения.

Проект от Bud Dietrich, AIA
4. Используйте пропорциональную систему, чтобы установить оптимальные размеры помещений
Высоту и ширину комнаты определите с использованием золотого сечения – техники, которая была разработана ещё тысячу лет назад.

Эскиз от Bud Dietrich, AIA
В этой комнате высота потолка и расположение декоративных панелей на кирпичной кладке стены было определено специалистом на основе мерных правил.
Принцип золотого сечения в строительстве дома. Золотое сечение в проектировании жилых домов
В древности люди осознавали, что окружающий их мир пребывает в гармонии и равновесии. Они прибегали к помощи мифов и религии, чтобы побольше узнать о порядке, которому подчинена природа. Сегодня мы обращаемся главным образом к ученым и математикам, чтобы они помогли нам объяснить то, что происходит в окружающем нас мире. Этот отказ от интуитивного и инстинктивного подхода и выражение большего доверия рациональным и интеллектуальным дисциплинам происходил постепенно. Однако был замечательный человек, который стоял в полный рост на перекрестке этих двух сил. Пифагор был выдающимся древнегреческим философом и математиком, который жил в VI веке до Рождества Христова. Он вывел теоремы, которые все мы изучаем и по сей день. Но, кроме этого, он также явился основоположником учения о сакральном значении чисел и математической науки. Согласно учению Пифагора, каждое число заключает в себе некий мистический компонент, который может быть осмыслен в процессе медитации и размышления. Он чувствовал, что понимание божественного значения математики открывает путь к тайнам всего космоса.
Одна из математических теорий Пифагора имеет огромное значение для дизайна наших домов. Он был убежден в том, что в природе существует органическая гармония, которая может быть выражена посредством чисел и пропорции, а также в то, что эти пропорции можно применять для строительства домов или других зданий. Используя принципы его теории Священной пропорции, можно «передвигать» энергию в своем доме из того места, где она ощущается как неблагополучная, в то место, где она начинает оказывать на вас благоприятное воздействие. Пропорции основаны на соотношении разных частей одного целого. Соотношение выражает разницу в размерах между двумя частями или свойствами. Оно определяет разницу между объектами или образами. Пропорции лежат в основе понятия об эстетике, позволяя уравновесить композицию, которая может создавать ощущение целостности и единства с окружающей средой.
Пифагор провозглашал совершенно определенные пропорциональные соотношения, которые он считал идеальными для благополучного существования людей. Он назвал это Золотой серединой (имея в виду, что такие пропорции представляют собой нечто среднее), Золотым сечением или Золотым прямоугольником. Эта магическая пропорция также иногда называется Священной пропорцией. Хотя древние архитекторы в культурных традициях всего мире уже были знакомы с магическим соотношением разных частей одного целого, Пифагор был тем человеком, который довел его до трансцендентного стандарта.
Такие пропорции, воплощенные в чем-либо, обычно радуют глаз, и они встречаются повсюду в естественной природе. Одним из примеров воплощения такой пропорции может быть раковина nautilus, где каждая отдельная часть идентична по форме той, которая следует за ней. И хотя они отличаются по размеру, все части имеют одинаковые пропорции, и все раковины имеют форму спирали, которая раскручивается из священной середины. Каждая часть раковины таким образом оставляет место для последующей части, являясь при этом воплощением магической спирали.
Золотое сечение также воплощено и в пропорциях человеческого тела. Известный рисунок Леонардо да Винчи, который соотносит пропорции тела человека с размерами
Можете объяснить по-простому, что такое золотое сечение и почему его так часто везде используют?
Золотое сечение — правило пропорции, не случайно его еще называют божественной гармонией.
Коротко эта пропорция определяется так: «меньшая часть относится к большей, как большая ко всему целому «.
В математике золотое сечение называют «асимметричной симметрией», оно выражается вполне конкретной формулой. Само понятие впервые использовал Пифагор, а число золотого сечения получило «имя» древнегреческого архитектора Фидия — число «фи» (греческая буква φ). Равно это число (с округлением) 1,62, а в процентном выражении золотое сечение выглядит, как 62% и 38%.
По канонам этой пропорции создавались произведения искусства еще древними египтянами, так что можно сказать, что золотое сечение сопровождает человеческую цивилизацию на протяжении всего ее развития.
Пропорции, если не совсем точные, то все же максимально близкие к золотому сечению, присутствуют везде — в искусстве, в природе и в самом человеке. Поэтому не совсем верно говорить, что его используют искуственно, оно просто является своеобразным маркером того, что красиво и гармонично.
Вот, например, можете и Вы убедиться, если измерите сами себя 🙂
Число «фи» или близкое к нему получится, если вычислить отношение расстояния от плеч до макушки к размеру головы; отношение расстояния от пупка до коленок и от коленок до ступней. И лицо воспринимается как более красивое, чем ближе его пропорции к идеальным: от подбородка до крайней точки верхней губы и от нее до носа пропорция близка к 1:1,62.
По правилу божественной гармонии «устроены» шишки, раковины моллюсков, чешуйки на плодах ананаса. Его обнаружили в молекуле ДНК и в спиралевидных галактиках.
Настоящие произведения искусства, которые человек подсознательно воспринимает, как прекрасные, тоже основаны на этой пропорции — будь это живопись, музыка, скульптура, архитектура и так далее.
Гармония в нашей жизни рулит! А гармония — это и есть золотое сечение 🙂
Гармонии и Вам!
ЗОЛОТОЕ СЕЧЕНИЕ В АРХИТЕКТУРЕ ДОМОВ
Исследовательская работа
тема: «Золотое сечение в архитектуре домов »
Автор: Буров Максим Николаевич
ученик 9 класса МОБУ СОШ с. Нижние Киги МР Кигинский район РБ
Руководитель:
Гизатуллин Алмаз Робертович
учитель математики МОБУ СОШ с. Нижние Киги МР Кигинский район РБ
Нижние Киги 2016
Оглавление
Введение …………………………………………………………………. 3
Методика исследования…………………………………………………. 5
Результаты исследований……………………………………………….. 8
Вывод……………………………………………………………………… 10
Заключение……………………………………………………………….. 11
Список использованной литературы…………………………………….. 12
Приложения ………………………………………………………………… 13
Введение
«…Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…».
Иоганн Кеплер
Цель проекта – применение «золотое сечение» при строительстве домов
Задачи:
1. Изучить понятия «пропорция»; «золотое сечение».
2. Исследовать присутствие золотого сечения в архитектуре.
3. Изучить практическое применение этого понятия, провести эксперименты с элементами золотого сечения.
4. Научиться анализировать и делать выводы.
Методы исследования:
1. Работа с учебной и научно-популярной литературой, ресурсами сети Интернет.
2. Наблюдения, эксперименты.
3. Сравнение, анализ, аналогия.
Объект исследования: «золотое сечение».
Предметы исследования: математика, архитектура.
Актуальность:
Так что же такое «золотое сечение»?.. Не все, наверное, обращали внимание, что окружающий мир строит свои «строение» по какому-то закону. Беспорядочность, бесформенность, несоразмерность воспринимаются нами как безобразное и производят отталкивающее впечатление. А предметы и явления, которым свойственна мера, целесообразность и гармония воспринимаются как красивое и вызывают у нас чувство восхищения, радости, поднимают настроение.
Людей с давних времён старались систематизировать и описать математически красоту форм. Можно ли «проверить алгеброй гармонию?» – как сказал А.С. Пушкин.
Конечно, не все формы красоты можно описать одной формулой, но, изучая математику, мы можем приблизиться к некоторой формуле прекрасного.
Я познакомился с одним из таких математических соотношений, там, где оно присутствует, ощущается гармония и красота.
Теорему Пифагора знают многие люди, а вот что такое «золотое сечение» – далеко не все. Нужно было ответить на вопрос «Что такое «золотая пропорция» или «золотое сечение»?
Об истории золотого сечения.
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.).
Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.
Платон (427…347 гг. до н.э.) также знал о золотом делении.
Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.
В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида.
Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Kампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре.
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет. «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать». Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии.6
Великий астроном XVI в. Иоганн Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение). Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».
Методика исследования
Я познакомился с понятием «золотое сечение», научился делить отрезок в золотом отношении, увидел, где оно встречается, как используется в технике и произведениях искусства.
Что же такое золотое сечение?
Рассмотрим отрезок АВ.
А С В
Его можно разделить точкой С на две части бесконечным множеством способов, но говорят что точка С производит золотое сечение отрезка АВ, если выполняется пропорция: длина меньшего отрезка так относится к длине большего, как больший отрезок относится к длине всего отрезка, т.е.
Термин золотое сечение ввёл в XVI веке великий художник, учёный и изобретатель Леонардо да Винчи. В истории утвердились три варианта названия: золотое сечение, золотая пропорция и третье – деление отрезка в среднем и крайнем отношениях. Кроме того, золотое сечение награждали эпитетами «божественное», «чудесное», «превосходнейшее», потому что-то, где оно присутствует, вызывает у нас ощущение красоты и гармонии.
Чтобы и вы смогли увидеть золотое сечение в природе, в произведениях искусства, я научу вас сейчас делить отрезок в среднем и крайнем отношениях, т.е. делить отрезок в золотом отношении.
D
E
C
B C A
Дано : Отрезок АВ.
Построить: золотое сечение отрезка АВ, то есть точку С так, чтобы
Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок Далее, соединив точки A и D, отложим отрезок DE=BD, и, наконец, AC=AE. Точка С является искомой, она производит золотое сечение отрезка АВ.
Деление отрезка в золотом отношении – это очень древняя задача. Она присутствует в «Началах» Евклида.
Золотое сечение записывается с помощью пропорции. Пропорция – это равенство двух отношений. Всем, я думаю, интересно узнать численное значение этих отношений. Сейчас мы его найдем.
Для удобства длину отрезка АВ обозначим за а , а длину отрезка АС – за х , то длина отрезка СВ будет а – х .
А х С а-х В
а
Пропорция (1) примет вид : (2).
(Отношение длины меньшего отрезка а – х к длине большего отрезка х равно отношению большего отрезка х к длине всего отрезка а).
Так как отношения составляющие пропорцию равны, то найдём численное значение, например, отношения Отношение длины меньшего отрезка к длине большего отрезка и отношение большего к длине всего отрезка равно 0,62 . Такое отношение и будет золотым. Полученное число обозначается буквой . Это первая буква в имени великого древнегреческого скульптора Фидия, жившего в V в до н.э., который часто использовал золотое отношение в своих произведениях.
На уроках геометрии мы изучали различные треугольники, оказывается, существует ещё так называемый золотой треугольник. Золотым называется такой равнобедренный треугольник , основание и боковая сторона которого находятся в золотом отношении:
В
А С
Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение ширины к длине даёт число 0,62, называется золотым прямоугольником.
L M
K N
В «золотом прямоугольнике» построим квадрат со стороной, равной меньшей стороне прямоугольника, у которого с прямоугольником общий прямой угол. Оказывается, снова получим золотой прямоугольник меньших размеров. В этом прямоугольнике снова построим квадрат, у которого с прямоугольником общий угол, и со стороной равной меньшей стороне прямоугольника. Снова получился золотой прямоугольник. Произведём несколько аналогичных построений.
Видим, что весь прямоугольник оказался составленным из вращающихся квадратов. Соединим противолежащие вершины квадратов плавной кривой. Сделаем это с помощью циркуля следующим образом…
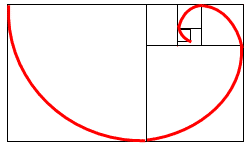
Мы получили кривую, которая является золотой спиралью .
Результаты исследований
Оказывается, в архитектуре встречаются и золотое сечение и его разновидности.
Некоторые предметы дают примеры золотого прямоугольника: обложки многих книг, журналов, тетрадей, открытки, картины, крышки столов, экраны телевизоров и т.д. близки по размерам к золотому прямоугольнику. [Приложение 1].
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.) Он имеет 8 колонн по коротким сторонам и 17 по длинным. выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. [Приложение 2].


Парфенон – это одно из красивейших произведений древнегреческой архитектуры. Он и сейчас, несмотря на то, что со времени его постройки прошло более 2,5 тысячелетий, производит огромное впечатление. Некогда белоснежный мрамор стал от времени золотисто-розовым. Величественное здание, стоящее на холме из известняка, возвышается над Афинами и их окрестностями. Но поражает оно не своими размерами, а гармоническим совершенством пропорций. Здание не вдавливается своей тяжестью в землю, а как бы парит над нею, кажется очень лёгким.
Многие искусствоведы стремились раскрыть секрет того могучего эмоционального воздействия, которое это здание оказывает на зрителя. Разгадку они увидели в том, что в соотношениях многих частей храма присутствует золотая пропорция. Так, отношение высоты здания к его длине равно 0,62 . Отношения целого ряда частей Парфенона дают число 0,62. Говорят «… у греческого храма нет размеров, у него есть пропорции …».
Другим примером из архитектуры древности является Пантеон. Известный русский архитектор М. Казаков в своем творчестве широко использовал “золотое сечение”. Его талант был многогранным, но в большей степени он раскрылся в многочисленных осуществленных проектах жилых домов и усадеб. Например, “золотое сечение” можно обнаружить в архитектуре здания сената в Кремле. По проекту М. Казакова в Москве была построена Голицынская больница, которая в настоящее время называется Первой клинической больницей имени Н.И. Пирогова. Еще один архитектурный шедевр Москвы – дом Пашкова – является одним из наиболее совершенных произведений архитектуры В. Баженова.

Скульпторы, архитекторы, художники использовали и используют золотое сечение в своих произведениях, так как пропорции золотого сечения создают впечатление гармонии и красоты.
Примеры архитектуры домов с Нижние Киги.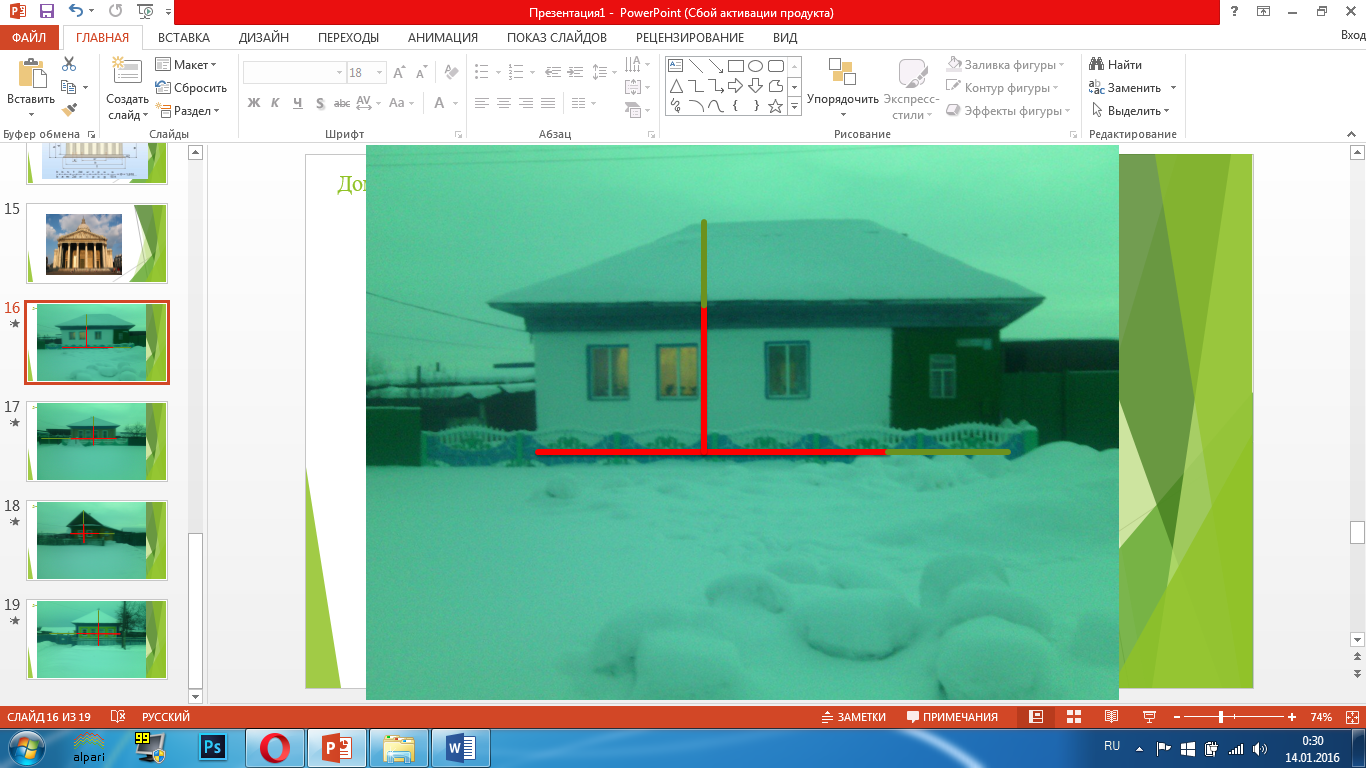
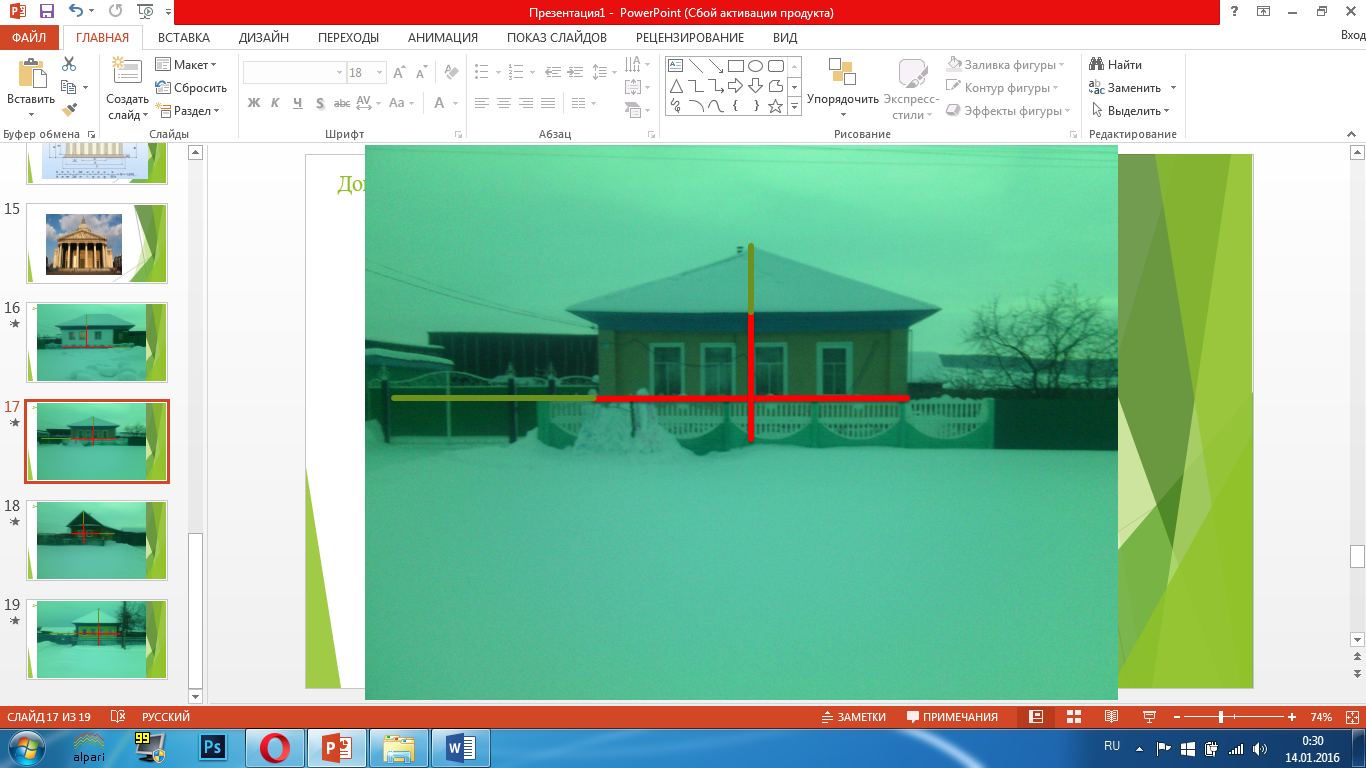
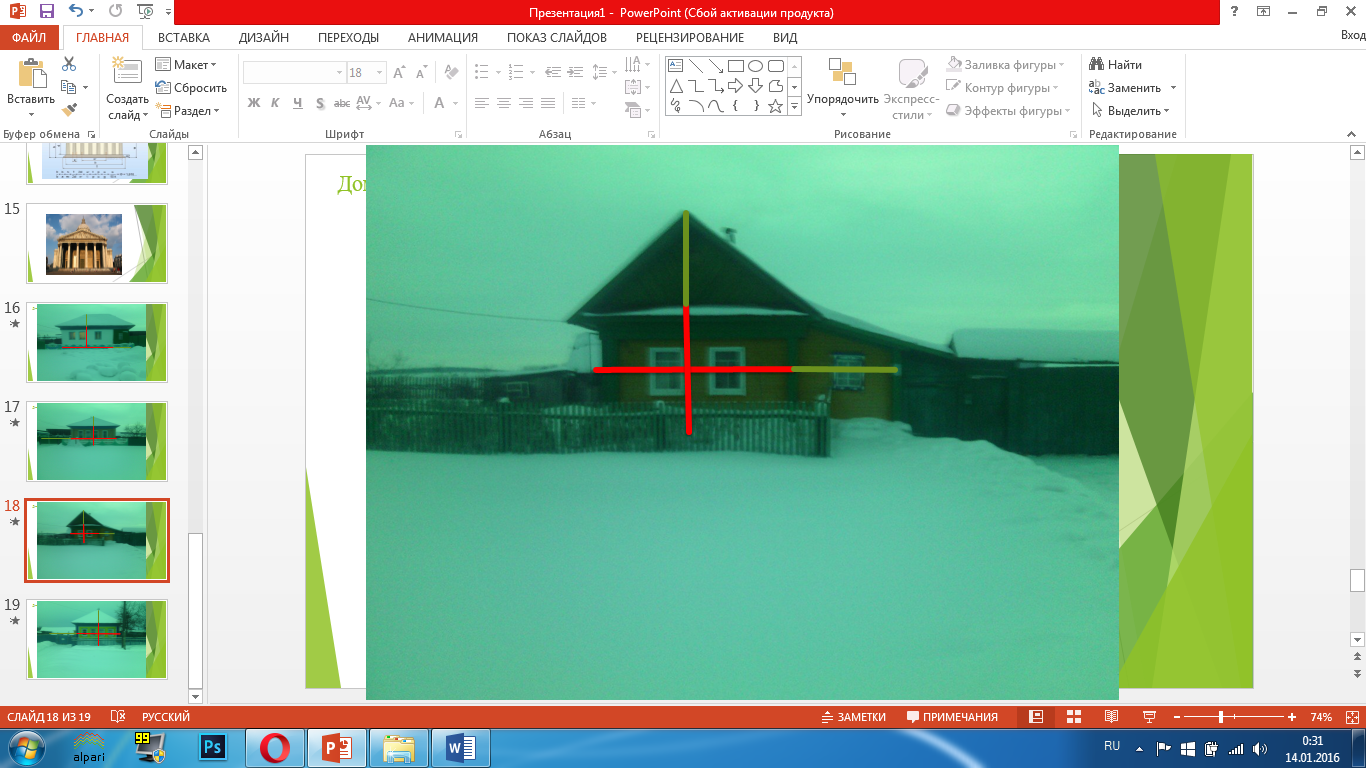
Из всего сказанного можно сделать выводы:
Золотое сечение является отображением окружающегося мира
Человеческое представление о красивом формировалось под влиянием порядка и гармонии
Закономерности «Золотого сечения» заложены в подсознании человека, они использовались и используются архитекторами в своих работах.
Заключение
В своей работе я рассмотрел пропорцию, научился делить отрезок в золотом отношении, изучил золотой треугольник, золотой прямоугольник, спираль. Исследовал архитектуры домов в селе на «золотое сечения».
В своей работе я хотел продемонстрировать красоту и широту «Золотого сечения» в реальной жизни. Проведенные исследования доказали, что большинство домов примерно удовлетворяют условию золотого сечения.
Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей различных простых фигур, эти части могут быть разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей.
Значение золотого сечения в современном мире в быту осознана не применяется, но инстинктивно люди стремиться к этому соотношению. Применения «золотого сечения» и других законов вытекающий из чисел Фибоначчи могут изменить не только красоту архитектурных сооружении, но и прочность его структуры.
ЛИТЕРАТУРА
Азевич А.И. Двадцать уроков гармонии: гуманитарно-математический курс. — М.: Школа-пресс, 1998.
Волошинов А.В. Математика и искусство. М., 1992.
https://ru.wikipedia.org/wiki/Золотое_сечение
http://www.abc-people.com/data/leonardov/zolot_sech-txt.htm
Приложение 1
«Золотой прямоугольник» учебников
учебникширина
а (см)
длина
в (см)
отношение
а/в
Русский язык
17
21
0,81
История России
14,7
21,5
0,68
Химия
16,5
21,7
0,76
Геометрия
14,5
21,5
0.67
Литература
14,7
22
0,668
Новая История
14,5
22
0,659
Биология 7 кл.
16,5
22
0,75
Английский язык
21
29,5
0,71
География
20
26,5
0,755
Физика
14,7
22
0,668
Дидактика геометрия
14
21,5
0,651
Дидактика алгебра
14
21
0,666
Дневник
16,8
21,5
0,781
Из исследования можно сделать вывод, что форма учебников близка к золотому прямоугольнику.
Приложение 2

Золотое сечение — Принципы формы и расположения
Теперь мы рассмотрим предмет, который исходит непосредственно из математики и который мы также можем найти повсюду, — золотое сечение . Не волнуйтесь; мы не вернемся в класс надолго. Мы рассмотрим, что это за концепция и насколько она является фундаментальной частью создания дизайна, приятного для глаз пользователя.
История золотого сечения стала легендой.Имея историю, восходящую почти ко времени Pi (еще одна великая математическая формула, которая необходима для понимания свойств кругов), ученые, в том числе Пифагор и Евклид, назвали ее многими именами, в том числе золотой серединой и божественный раздел .
В чем привлекательность этого соотношения? На протяжении веков считалось, что искусство, архитектура и природа более привлекательны для глаз, когда пропорции конструкций и сооружений основаны на золотом сечении.Вы можете найти примеры золотого сечения в деятельности человека еще в Древней Греции. Статуи Парфенона, кажется, демонстрируют золотое сечение в своей форме, и некоторые из пяти тел Платона (включая куб и додекаэдр) тоже связаны с ним. Золотое сечение было популяризировано в эпоху Возрождения, и художники того периода стремились использовать его для создания эстетически привлекательных работ. Сегодня мы можем использовать золотое сечение в дизайне наших веб-сайтов и приложений для улучшения макета и привлекательности для глаз, полностью доверяя этому проверенному временем факту.
Что такое золотое сечение?
Золотое сечение использовалось на протяжении всей истории для создания визуально привлекательных дизайнов. В эпоху Возрождения это стало формализованной частью теории дизайна. Его частое появление в геометрии (в форме пятиугольника и пентаграммы) привлекло внимание древнегреческих математиков, которые начали изучать его не менее 2400 лет назад. Отношение основано на соотношении между последовательными числами в последовательности Фибоначчи.Фибоначчи был средневековым итальянским математиком; однако вам не нужно быть математиком, чтобы понять эту последовательность, поскольку она настолько проста.
Каждое число в последовательности Фибоначчи — это просто сумма двух чисел перед ним. Он начинается с 1, 1 (т. Е. 1 + невидимый 0 = 1), а первые 10 членов последовательности — это 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. Он продолжается бесконечно. . Мы можем рассчитать соотношение, используя формулу выше (мы используем греческую букву Phi для обозначения вывода).Отношение составляет примерно 1,618, хотя, как и Pi , оно имеет длинную строку чисел после десятичной точки. Однако для наших целей нам не нужно беспокоиться о выходе за пределы 1.618.
Как соотношение используется в дизайне? Представьте себе прямоугольник с короткой стороной длиной 1. Чтобы вычислить наиболее эстетичный прямоугольник, вы просто умножаете длину короткой стороны на приближение золотого сечения 1,618. Таким образом, в данном случае длинная сторона будет иметь длину 1.618.
Если у вас есть карандаш, бумага и линейка, попробуйте нарисовать прямоугольник такого масштаба. Или, если вы можете перейти на другой экран, создайте его в приложении для рисования. То, что вы увидите перед собой, — это не просто прямоугольник, а идеальный прямоугольник !
Золотое сечение можно найти во всем мире дизайна. Архитекторы того времени использовали его для основания и высоты Акрополя в Греции. Он используется для определения формата подавляющего большинства книг на вашем физическом книжном шкафу.Это буквально везде, куда ни глянь. Возможно, потому, что мы окружены фигурами и формами, полученными из золотого сечения, мы особенно привыкли к нему. Как дизайнеры, мы должны помнить об этой концепции комфорта и удобства для наших пользователей. Глаза мира благосклонно относятся к этому соотношению. Фактически, буквально: в журнале National Geographic используется желтый прямоугольник, пропорциональный золотому сечению.
Однако золотое сечение не помогает нам просто создавать красивые прямоугольники.Вы также можете сформировать спираль, используя длины сторон, основанные на порядке убывания последовательности Фибоначчи. Итак, если мы возьмем длину 55 в качестве отправной точки, мы можем сделать нашу спираль, потянув ее внутрь, так что, когда она пройдет эту начальную точку, новая длина будет 34. Мы продолжаем работать внутрь с длинами 21, 13, 8, 5 и т.д., пока не дойдем до середины (длина = 1). Эта спираль также основана на золотом сечении и может быть более интересной для человеческого глаза, чем столь же сбалансированная спираль. Он присутствует в природе, от растений до моллюсков.Часто говорят, что даже определенные пропорции многих более крупных животных (включая людей!) Пропорциональны золотому сечению. В этом смысле можно сказать, что это часть нас. Таким образом, вы, как дизайнер, можете использовать эту спираль, чтобы привлечь внимание пользователей из любой части мира и сосредоточить их на определенной точке вашего дизайна. Исследования показали, что человеческий глаз распознает (а мозг интерпретирует и обрабатывает) изображения, основанные на золотом сечении, быстрее, чем изображения, которые не включают это соотношение.
Мы также можем использовать золотое сечение, чтобы сбалансировать элементы в других элементах. Логотипы Toyota и Pepsi используют этот факт. Toyota использует соотношение, чтобы сбалансировать овалы в своем логотипе, а Pepsi использует его, чтобы сбалансировать круги в своем логотипе. Можете ли вы назвать другие бренды, которые используют это «волшебное» соотношение? Возможно, это то, что может сделать логотипы по-настоящему знаковыми!
Расчет золотого сечения
Давайте теперь вкратце перейдем к математике. Как и в случае с изображением, показанным в верхней части этого урока, уравнение для расчета отношения простое.Это соотношение между двумя сторонами дизайна (обычно горизонтальной и вертикальной). Неважно, какую сторону мы выберем как самую длинную (A), а какую — как самую короткую (B). (Хотя, если вы пытаетесь увидеть, использовалось ли золотое сечение в другом произведении, вам нужно будет проследить, какая сторона самая длинная или самая короткая.)
Формула для этого:
A / B = (A + B) / A = 1,618033987 = Φ
Φ — это греческая буква Phi — , как мы представляем золотое сечение. Почему делает A / B = (A + B) / A? Это происходит потому, что мы следуем последовательности Фибоначчи, а A и B (если они выражены целыми числами) — это просто два последовательных числа в этой последовательности. К счастью, мы можем приблизить это к 1,6, 1,61 или 1,618 в дизайне, не отказываясь от эстетической привлекательности золотого сечения. Наши глаза не беспокоят такие незначительные отклонения.
Как использовать золотое сечение в ваших проектах
Вы можете легко использовать золотое сечение в своих проектах.Используя такие приложения, как Adobe Photoshop и Adobe Illustrator, вы можете создавать направляющие или слои, которые помогут вам создавать дизайн с использованием золотого сечения.
Если ваше программное обеспечение не вычисляет золотое сечение автоматически, вы всегда можете использовать онлайн-инструмент, чтобы помочь указать соотношение длин сторон. Вот три таких инструмента:
GoldenRATIO
Фикалкулятор
Atrise Золотое сечение
The Take Away
Золотое сечение, которое философы, математики, архитекторы, художники и дизайнеры использовали более двух тысяч лет, является фундаментальным как для дизайнеров, так и для пользователей.Нас окружают такие узоры, как логотип Pepsi, и даже естественные образования, несущие пропорции золотого правила, такие как раковина наутилуса.
Поскольку эти формы настолько распространены, наши глаза быстро распознают их, и мы склонны воспринимать их как знакомые и приятные. Хотя золотое сечение было предметом изучения на протяжении веков и было известно древним грекам, средневековый итальянский математик Фибоначчи определил свою знаменитую последовательность. Использование этого (где ряд чисел, начинающийся с 1,1, таков, что мы добавляем предыдущее число к следующему) является ключом к пониманию золотого сечения (которое мы представляем греческой буквой Phi ).
Мы широко используем золотое сечение в веб-дизайне и дизайне приложений. В частности, его очень легко использовать при создании каркасов. Вы можете убедиться, что необходимый вам контент правильно расставлен по приоритетам и что эстетические требования макета будут удовлетворены, не выполняя сначала слишком много дизайнерской работы. Только когда вы, например, решите, где вы будете размещать элементы и функции в этой структуре, работа станет более сложной.
На верхнем изображении в приведенном выше примере соотношение между областью содержимого и боковой панелью равно Phi (1.618). Вы можете проверить это с помощью измерений ниже:
- Общая ширина фиксированного макета — 960 пикселей. Вы разделяете это на область содержимого и боковую панель. Область содержимого является более длинной из двух областей.
- Если вы разделите общую ширину 960 пикселей на 1,618, вы получите 593 пикселей. Затем вы назначаете эту длину области содержимого.
- Вы назначаете оставшиеся 367 пикселей боковой панели.
Поскольку это соотношение, оно гибкое. Это означает, что вы можете легко применить его для создания множества макетов дизайна, так как нет необходимости использовать фиксированные числа.Все, что вам нужно сделать, это указать, что более длинная область в 1,618 раза длиннее, чем более короткая.
Золотое сечение можно применить к любой части макета страницы. Например, вы можете использовать золотое сечение в заголовке, чтобы привлечь внимание пользователя, а затем повторить его и в теле.
На нижнем рисунке (вверху) мы также видим спиральную форму, в которой используется золотое сечение. Используя последовательность Фибоначчи в порядке убывания применительно к длинам стороны спирали, мы можем легко создавать спиральные конструкции на основе золотого сечения.
Как дизайнеры, мы находим множество доступного программного обеспечения, которое упрощает нам раскрытие потенциала золотого сечения в наших творениях и оптимизирует взаимодействие с пользователем. Adobe с Photoshop и Illustrator — такая компания, предлагающая такую большую помощь.
Ссылки и где узнать больше
- Изображение героя: Автор / Правообладатель: Мэтью Олифант. Условия авторских прав и лицензия: CC BY-ND 2.0
- Фридман, В.(2008) Применение божественной пропорции к вашим веб-дизайнам. Smashing Magazine. Получено с: http://www.smashingmagazine.com/2008/05/29/applying-divine-proportion-to-web-design/. [1 августа 2014 г.]
История золотого сечения
Хотя пропорция, известная как золотое сечение, всегда существовала в математике и в физической вселенной, точно неизвестно, когда она была впервые открыта и применена человечеством. Разумно предположить, что он, возможно, был обнаружен и повторно открыт на протяжении всей истории, что объясняет, почему он имеет несколько названий.
Использование в архитектуре относится к древним египтянам и грекам
Похоже, что египтяне могли использовать и пи, и фи в дизайне Великих пирамид.Некоторые считают, что греки основали дизайн Парфенона на этой пропорции, но это является предметом некоторых предположений.
Фидий (500 г. до н.э. — 432 г. до н.э.), греческий скульптор и математик, изучил фи и применил его к дизайну скульптур для Парфенона.
Платон (около 428 г. до н.э. — 347 г. до н.э.) в своих взглядах на естествознание и космологию, изложенных в его «Тимее», считал золотое сечение наиболее связывающим из всех математических соотношений и ключом к физике космоса.
Евклид (365 г. до н.э. — 300 г. до н.э.) в «Элементах» упоминает разделение линии в точке 0,6180399… как «разделение линии в крайнем и среднем соотношении». Позже это привело к использованию термина «среднее значение» в золотой середине. Он также связал это число с построением пентаграммы.
Ряд Фибоначчи был открыт около 1200 г. н.э.
Леонардо Фибоначчи, итальянец, родившийся в 1175 году нашей эры (2), обнаружил необычные свойства числового ряда, который теперь носит его имя, но не факт, что он вообще осознавал его связь с фи и золотой серединой.Его наиболее заметным вкладом в математику была работа, известная как Liber Abaci, которая оказала решающее влияние на принятие европейцами арабской десятичной системы счета над римскими цифрами. (3)
Впервые он был назван «Божественной пропорцией» в 1500-х годах.
 Леонардо да Винчи представил иллюстрации к диссертации, опубликованной Лукой Пачоли в 1509 году под названием «De Divina Proportione» (1), возможно, самой ранней ссылкой в литературе на другое ее название, «Божественная пропорция».Эта книга содержит рисунки пяти Платоновых тел, сделанные Леонардо да Винчи.
Леонардо да Винчи представил иллюстрации к диссертации, опубликованной Лукой Пачоли в 1509 году под названием «De Divina Proportione» (1), возможно, самой ранней ссылкой в литературе на другое ее название, «Божественная пропорция».Эта книга содержит рисунки пяти Платоновых тел, сделанные Леонардо да Винчи.
Художники эпохи Возрождения широко использовали золотую середину в своих картинах и скульптурах для достижения баланса и красоты. Леонардо да Винчи, например, использовал его, чтобы определить все основные пропорции своей картины «Тайная вечеря», от размеров стола, за которым сидели Христос и ученики, до пропорций стен и окон на заднем плане.
Иоганн Кеплер (1571-1630), открывший эллиптическую природу орбит планет вокруг Солнца, также упомянул «Божественную пропорцию», сказав о ней следующее:
«В геометрии есть два великих сокровища: одно — это теорема Пифагора; другой — разделение линии на крайнее и среднее соотношение.Первое мы можем сравнить с мерой золота; второй мы можем назвать драгоценным камнем ».
«Золотое сечение» было введено в 1800-е годы.
Считается, что Мартин Ом (1792–1872) был первым, кто использовал термин «золотой» для описания золотого сечения. использовать этот термин. В 1815 году он опубликовал «Die reine Elementar-Mathematik» (Чистая элементарная математика). Эта книга известна тем, что в ней впервые встречается термин «goldener schnitt» (золотое сечение).
Термин «фи» не использовался до 1900-х годов.
Только в 1900-х годах американский математик Марк Барр использовал греческую букву фи (Φ) для обозначения этой пропорции.Это появилось в «Кривых жизни» (стр. 420) в 1914 году Теодора Андреа Кук. К тому времени эта вездесущая пропорция была известна как золотая середина, золотое сечение и золотое сечение, а также Божественная пропорция. Фи — первая буква Фидия (1), который использовал золотое сечение в своих скульптурах, а также греческий эквивалент буквы «F», первой буквы Фибоначчи. Фи также является 21-й буквой греческого алфавита, а 21 — одним из чисел в ряду Фибоначчи. Иероглиф для фи также имеет некоторые интересные богословские значения.
Последние появления Фи в математике и физике
Phi продолжает открывать новые двери в нашем понимании жизни и Вселенной. Он появился в открытии Роджера Пенроуза в 1970-х годах «Плитки Пенроуза», которая впервые позволила укладывать поверхности плиткой с пятикратной симметрией. Он снова появился в 1980-х годах в квазикристаллах, недавно открытой форме материи.
Фи как дверь к пониманию жизни
Описание этой пропорции как Золотой и Божественной, возможно, уместно, потому что многие считают ее открывающей дверь к более глубокому пониманию красоты и духовности в жизни.Это невероятная роль для одного числа, но, опять же, это одно число сыграло невероятную роль в истории человечества и во Вселенной в целом.
Источник — Божественная пропорция: Исследование математической красоты Х. Э. Хантли
(1) Стр.25
(2) Стр.157
(3) Стр.158
Золотое сечение — подробное объяснение
Золотое сечение, также известное как золотая пропорция, золотая середина, золотое сечение, золотое число и божественная пропорция, представляет собой деление данной единицы длины на две части таким образом, чтобы отношение более короткого к более длинному равняется отношению более длинной части к целому или, когда линия разделена таким образом, что отношение более длинной части линии к целому точно такое же, как отношение более короткой части линии к более длинной часть.
Это число часто встречается при определении отношения расстояний в простых геометрических фигурах, таких как пятиугольник, пентаграмма, десятиугольник и додекаэдр.Это соотношение или пропорция, определяемая числом Phi = 1,618033988749895 … Это иррациональное число, то есть это число, которое нельзя записать в виде простой дроби — десятичная дробь продолжается бесконечно, не повторяя. Фи, как и Пи, представляет собой отношение, определяемое геометрической конструкцией.
Точно так же, как Pi — это отношение длины окружности к ее диаметру, Phi — это просто отношение отрезков линии, которые возникают при разделении линии одним очень особым и уникальным способом.
Фигура золотого сечения иллюстрирует геометрическую связь, определяющую эту константу.Выражается алгебраически:

Уникальное положительное решение этого уравнения — алгебраическое иррациональное число 
Формы, пропорциональные золотому сечению, долгое время считались эстетически приятными во многих культурах и до сих пор часто используются в искусстве и дизайне, что предполагает естественный баланс между симметрией и асимметрией.
Древние пифагорейцы, которые определяли числа как выражения соотношений (а не как единицы, как это принято сегодня), считали, что реальность является числовой и что золотое сечение выражает основную истину о существовании.
Золотое сечение, кажется, получило свое название от Золотого Прямоугольника, прямоугольника, стороны которого пропорциональны Золотому сечению.
Теория Золотого Прямоугольника — эстетическая, что соотношение является эстетически приятным и поэтому может быть обнаружено спонтанно или намеренно в большом количестве произведений искусства. Фасад Парфенона удобно оформить золотым прямоугольником. Дополнительные классические части прямоугольника идеально сочетаются с основными архитектурными особенностями строения.

Золотой прямоугольник можно использовать для создания спирали, Золотой спирали. Начиная с одного золотого прямоугольника, второй золотой прямоугольник можно прикрепить к первому, используя самую длинную сторону прямоугольника, сторону A как самую короткую сторону B следующего прямоугольника. Для этого второй прямоугольник строится под углом 90 градусов перпендикулярно первому прямоугольнику. Если продолжить этот процесс, называемый спиралью Золотого прямоугольника, через углы прямоугольников можно провести изогнутую линию, образуя спираль Золотого сечения.Спираль золотой середины продолжается бесконечно во внутреннем и внешнем направлениях, она становится все меньше и меньше по спирали внутрь и все больше и больше по спирали наружу.
Другая связь золотого сечения с частичными симметриями в природе — через числа Фибоначчи. Это числовой ряд, в котором каждый член представляет собой просто сумму двух предыдущих чисел. Спирали Фибоначчи и отношения золотого сечения появляются повсюду во Вселенной. Спираль — это естественная форма потока воды, когда она стекает в канализацию.Это также естественная форма потока воздуха во время торнадо и ураганов. Вот еще один прекрасный пример спирали Фибоначчи в природе — это оболочка Наутилуса, и каждая книга о сакральной геометрии содержит ее: 
Размеры Великой пирамиды Гизы также основаны на золотом сечении. Если мы возьмем поперечное сечение Великой пирамиды, мы получим прямоугольный треугольник, так называемый Египетский треугольник. Отношение наклонной мета-высоты пирамиды (гипотенузы треугольника) к расстоянию от центра земли (половина размера основания) равно 1.61804 … который отличается от фи только на одну единицу пятого знака после запятой. Если мы допустим базовое измерение равным 2 единицам, то стороны прямоугольного треугольника будут иметь пропорцию 1: sqrt (phi): phi, а мета-высота пирамиды будет равна sqrt (phi). 
Леонардо да Винчи демонстрировал золотое сечение во многих своих картинах и иллюстрациях, назвав его De Divina Proportione или «божественная пропорция». Он провел полное исследование человеческого тела и соотношения длин различных частей тела.

© Token Rock, Inc. Все права защищены.
.Коэффициент золотого сечения— Видеоурок Академии рисования
Обнаружение коэффициента золотого сечения
Описание видеоурока
В этом видеоуроке вы откроете для себя соотношение золотого сечения, также известное как золотая пропорция, золотое сечение, божественная пропорция, золотое сечение или золотое сечение, которое является универсальным принципом, присутствующим в природе, науке и искусстве.

Получите бесплатные видеоуроки
Получите бесплатные видеоуроки
Соотношение золотого сечения — божественная формула, управляющая изобразительным искусством
Коэффициент золотого сечения математически определяется природой и используется художниками, скульпторами и архитекторами в качестве ориентира для красоты и гармонии.Греческий символ Фи используется для обозначения соотношения золотого сечения .
Давайте рассмотрим соотношение золотого сечения, чтобы понять, как оно работает, сравнив два отношения, описанных известным греческим математиком Евклидом Александрийским около 2300 лет назад.
В своей книге «Элементы» Евклид провел линию и разделил ее на соотношение, которое он назвал «крайним и средним соотношением».
Линия «A» разделена на две части «B» и «C», так что отношение линии «A» к большей части «B» такое же, как отношение части «B» к меньшей части « C ».
Это соотношение золотого сечения Phi можно рассчитать как сумму 1, добавленную к квадратному корню из 5, деленную на 2, и получится примерно 1,61803: 1.
Используя соотношение золотого сечения Евклида, мы можем исследовать пентаграмму. Все сегменты пентаграммы в порядке убывания длины находятся в соотношении золотого сечения Phi, равном 1,816.
 Природа использует те же принципы построения. Давайте разрежем яблоко, чтобы проверить участки пентаграммы в центре. Эта форма представляет собой пятиконечную звезду, которую еще называют «Пентада»; на протяжении веков он считался символом власти.Первое письменное описание этого символа можно найти в книге Луки Пачоли, учителя Леонардо да Винчи, который открыл миру метод построения пентад и ее уникальные геометрические свойства.
Природа использует те же принципы построения. Давайте разрежем яблоко, чтобы проверить участки пентаграммы в центре. Эта форма представляет собой пятиконечную звезду, которую еще называют «Пентада»; на протяжении веков он считался символом власти.Первое письменное описание этого символа можно найти в книге Луки Пачоли, учителя Леонардо да Винчи, который открыл миру метод построения пентад и ее уникальные геометрические свойства.Геометрия пентады также может быть найдена в семенах, листьях, цветах, морских звездах и многих других растениях и живых существах.
Золотое сечение встречается в природе в виде спиралей. Равноугольная спираль, также известная как «Spira Mirabilis», представляет собой логарифмическую спираль.Расстояния между рукавами этой спирали увеличиваются в геометрической прогрессии. Его можно построить геометрически с использованием золотых треугольников или золотых прямоугольников пропорции золотого сечения.
В природе существует бесконечное количество примеров сечения золотого сечения и золотых спиралей. Его геометрия даже объясняет, почему в эпицентре бури спокойно, а ураган может достигать сотни миль в час по скорости ветра. Глаз золотой спирали называется Асимптотой. Это то место, к которому спираль приближается, но никогда не достигает; таким образом, силы ветра в эпицентре бури находятся в равновесии.
Спираль с золотым сечением работает и в космическом масштабе. Спиральные галактики образуются вокруг центра тяжести, но подчиняются одним и тем же божественным законам.
В наших телах можно найти множество спиралей. Примеры этих спиральных форм включают человеческое ухо, наши кулаки, человеческий эмбрион и структуру нашей ДНК.
Человеческое тело и пропорции лица следуют божественной формуле.
Знаменитый рисунок Леонардо да Винчи «Витрувианский человек», датируемый 1509 годом, изображает человека в двух наложенных друг на друга позах, с руками и ногами, вписанными в квадрат и круг.Круг с центром в его центре тяжести, пупке, и квадрат с центром в основании его пениса. Колени мужчины, основание пениса и середина груди делят фигуру на 4 равные части.
Этот рисунок назван в честь Марка Витрувия Поллиона, римского архитектора, писателя и инженера, который около 2040 лет назад написал:
• Длина раскинутых рук равна росту человека;
• Потому что человеческое тело устроено природой так, что лицо от подбородка до верхней части лба и самых нижних корней волос составляет десятую часть всего роста;
• Открытая рука от запястья до кончика среднего пальца такая же;
• Голова от подбородка до макушки восьмая;
• От груди до линии роста волос одна седьмая человеческого роста;
• И с шеей и плечом от верха груди до нижних корней волос — шестая часть;
• От середины груди до вершины макушки проходит четверть;
• Максимальная ширина плеч — четверть роста мужчины;
• Расстояние от локтя до кончика руки составляет четверть роста человека;
• Расстояние от локтя до подмышки составляет одну восьмую роста мужчины;
• Корень полового члена составляет половину роста мужчины;
• ступня составляет одну седьмую роста человека;
• Расстояние от подбородка до носа, бровей и линии роста волос равно ушам и одной трети лица.
Пропорции человеческого тела соотносятся с пропорцией золотого сечения Фи.
• Соотношение золотого сечения можно найти в соотношении расстояния между кончиком пальца и локтем к расстоянию между запястьем и локтем;
• Отношение расстояния между пупком и концом стопы к расстоянию между пупком и коленом;
• Отношение расстояния между пупком и макушкой головы к расстоянию между пупком и линией плеч;
• Отношение расстояния между пупком и макушкой головы к расстоянию между макушкой и серединой груди.
На протяжении веков пропорции золотого сечения человеческого тела восхищали художников. Альбрехт Дюрер, немецкий художник, график и гуманист, написал, проиллюстрировал и отредактировал книгу о пропорциях человеческого тела. Эта книга была разработана, чтобы применить науку об анатомических пропорциях человека к эстетике.
То же золотое сечение
.